题目内容
（2012•镇江）如图，在平面直角坐标系xOy中，直线AB经过点A（-4，0）、B（0，4），⊙O的半径为1（O为坐标原点），点P在直线AB上，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为| 7 |
| 7 |
分析：连接OP．根据勾股定理知PQ2=OP2-OQ2，当OP⊥AB时，线段OP最短，即线段PQ最短．
解答：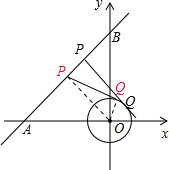
解：连接OP、OQ．
∵PQ是⊙O的切线，
∴OQ⊥PQ；
根据勾股定理知PQ2=OP2-OQ2，
∵当PO⊥AB时，线段PQ最短；
又∵A（-4，0）、B（0，4），
∴OA=OB=4，
∴AB=4
∴OP=
AB=2
，
∴PQ=
；
故答案是：
．
解：连接OP、OQ．∵PQ是⊙O的切线，
∴OQ⊥PQ；
根据勾股定理知PQ2=OP2-OQ2，
∵当PO⊥AB时，线段PQ最短；
又∵A（-4，0）、B（0，4），
∴OA=OB=4，
∴AB=4
| 2 |
∴OP=
| 1 |
| 2 |
| 2 |
∴PQ=
| 7 |
故答案是：
| 7 |
点评：本题考查了切线的判定与性质、坐标与图形性质以及矩形的性质等知识点．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角来解决有关问题．
练习册系列答案
相关题目
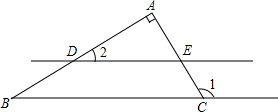（2012•镇江）如图，∠1是Rt△ABC的一个外角，直线DE∥BC，分别交边AB、AC于点D、E，∠1=120°，则∠2的度数是
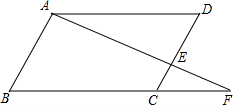（2012•镇江）如图，E是?ABCD的边CD上一点，连接AE并延长交BC的延长线于点F，且AD=4，
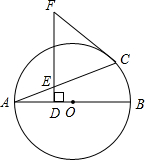（2012•镇江）如图，AB是⊙O的直径，DF⊥AB于点D，交弦AC于点E，FC=FE．
（2012•镇江）如图，在平面直角坐标系xOy中，直线y=2x+n与x轴、y轴分别交于点A、B，与双曲线y=