题目内容
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴,点C在y轴的正半轴上,点F再AB上,点B,E在反比例函数y= ![]() 的图象上,OA=2,OC=6,则正方形ADEF的边长为 .
的图象上,OA=2,OC=6,则正方形ADEF的边长为 . 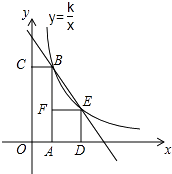
【答案】![]() ﹣1
﹣1
【解析】解:∵OA=2,OC=6, ∴B点坐标为(2,6),
∴k=2×6=12,
∴反比例函数解析式为y= ![]() ,
,
设AD=t,则OD=2+t,
∴E点坐标为(2+t,t),
∴(2+t)t=12,
整理为t2+2t﹣12=0,
解得t1=﹣1+ ![]() (舍去),t2=﹣1﹣
(舍去),t2=﹣1﹣ ![]() ,
,
∴正方形ADEF的边长为 ![]() ﹣1.
﹣1.
故答案为: ![]() ﹣1.
﹣1.
先确定B点坐标(2,6),根据反比例函数图象上点的坐标特征得到k=12,则反比例函数解析式为y= ![]() ,设AD=t,则OD=2+t,所以E点坐标为(2+t,t),再根据反比例函数图象上点的坐标特征得(2+t)t=12,利用因式分解法可求出t的值.
,设AD=t,则OD=2+t,所以E点坐标为(2+t,t),再根据反比例函数图象上点的坐标特征得(2+t)t=12,利用因式分解法可求出t的值.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目