题目内容
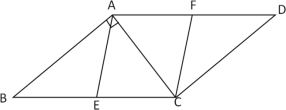
【题目】如图,平行四边形ABCD中,AP,BP分别平分∠DAB和∠CBA,交于DC边上点P,AD=5.
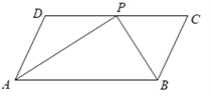
(1)求线段AB的长.
(2)若BP=6,求△ABP的周长.
【答案】(1)10cm;(2)24cm.
【解析】
(1)根据角平分线定义和平行线性质得∠DAP=∠BAP,∠DPA=∠PAB,等量代换得∠DAP=∠DPA,由等腰三角形性质可得DA=DP ;同理可得 CB=CP,由DC=DP+CP即可求得答案.
(2)据角平分线定义得∠BAP=![]() ∠BAD,∠PBA=
∠BAD,∠PBA=![]() ∠CBA, 由平行线性质得∠DAB+∠ABC=180°,从而可得 ∠PAB+∠PBA=90°,在Rt△APB中,根据勾股定理求得AP长,再由三角形周长即可求得答案.
∠CBA, 由平行线性质得∠DAB+∠ABC=180°,从而可得 ∠PAB+∠PBA=90°,在Rt△APB中,根据勾股定理求得AP长,再由三角形周长即可求得答案.
解:(1)在平行四边形ABCD中,
∵AP平分∠DAB,
∴∠DAP=∠BAP,
∵DC//AB,
∴∠DPA=∠PAB,
∴∠DAP=∠DPA,
∴DA=DP.
同理CB=CP,
∴AD=BC=5,
∴DC=DP+CP=10cm.
(2)∵DA//CP,
∴∠DAB+∠ABC=180° ,
∵AP平分∠DAB,BP平分∠ABC
∴∠BAP= ![]() ∠BAD,∠PBA=
∠BAD,∠PBA= ![]() ∠CBA,
∠CBA,
∴∠PAB+∠PBA=90,
∴∠APB=90,
∵AB=10,BP=6,
∴PA=8,
∴C△ABP=24cm.

练习册系列答案
相关题目