题目内容
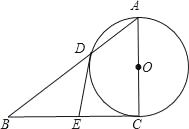
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E,构造出平行四边形AEDF.
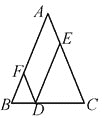
(1)若点D在线段BC上时. ①求证:FB=FD.②求证:DE+DF=AC.
(2)点D在边BC所在的直线上,若AC=8,DE=3,请作出简单示意图求DF的长度,不需要证明.
【答案】(1)见解析,见解析;(2)DF=BF=5或DF=BF=11 见解析.
【解析】
(1)①根据等腰三角形性质得∠B=∠C,由平行线性质得∠FDB=∠C,等量代换得∠B=∠FDB,根据等腰三角形性质:等角对等边即可得证.
②由平行四边形性质得ED=AF,AE=FD,由①知FB=FD,等量代换得AE=FB,从而可得DE+DF= AF+ FB=AB=AC.
(2)如图1:根据平行四边形性质得AF=DE=3,DF=AE,由(1)知FB=FD,由DF=BF=AB-AF=8-3=5;
如图2:根据平行四边形性质得AF=DE=3,DF=AE,由(1)知FB=FD,由DF=BF=AB+AF=8+3=11.
解:(1)①∵AB=AC,
∴∠B=∠C,
∵DF//AC,
∴∠FDB=∠C,
∴∠B=∠FDB,
∴FB=FD.
②∵四边形AEDF是平行四边形,
∴ED=AF,AE=FD,
∵FB=FD,
∴AE=FB,
∴DE+DF= AF+ FB=AB,
∵AB=AC,
∴DE+DF=AC.
(2)如图1,

∵四边形AEDF为平行四边形,
∴AF=DE,DF=AE,
由(1)知FB=FD,
∵AC=8,DE=3,AB=AC,
∴AF=3,BF=AB-AF=8-3=5,
∴DF=BF=5;
如图2,

∵四边形AEDF为平行四边形,
∴AF=DE,DF=AE,
由(1)知FB=FD,
∵AC=8,DE=3,AB=AC,
∴AF=3,BF=AB+AF=8+3=11,
∴DF=BF=11;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案