题目内容
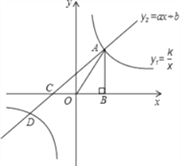
【题目】如图,已知反比例函数y1=kx-1和一次函数y2=ax+b的图象相交于点A和点D,且点A的横坐标为1,点D的纵坐标为-1.过点A作AB⊥x轴于点B,△AOB的面积为1.
(1)求反比例函数和一次函数的解析式.
(2)若一次函数y2=ax+b的图象与x轴相交于点C,求∠ACO的度数.
(3)结合图象直接写出:当y1>y2时,x的取值范围.
【答案】(1)![]() ;y2=x+1;(2)45°;(3)0<x<1.
;y2=x+1;(2)45°;(3)0<x<1.
【解析】试题分析:此题考查了运用待定系数法求函数解析式及运用函数图象解不等式,属基础题型.
(1)根据△AOB的面积可求AB,得A点坐标.从而易求两个函数的解析式;
(2)求出C点坐标,在△ABC中运用三角函数可求∠ACO的度数;
(3)观察第一象限内的图形,反比例函数的图象在一次函数的图象的上面部分对应的x的值即为取值范围.
试题解析:解:(1)∵△AOB的面积为1,并且点A在第一象限,
∴k=2,∴y1=2x;
∵点A的横坐标为1,
∴A(1,2).
把A(1,2)代入y2=ax+1得,a=1.
∴y2=x+1.
(2)令y2=0,0=x+1,
∴x=-1,∴C(-1,0).
∴OC=1,BC=OB+OC=2.
∴AB=CB,∴∠ACO=45°.
(3)由图象可知,在第一象限,当y1>y2>0时,0<x<1.在第三象限,当y1>y2>0时,-1<x<0(舍去).

练习册系列答案
相关题目