题目内容
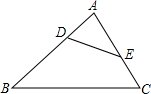如图，D、E两点分别在△ABC的边AB、AC上，DE与BC不平行．（1）补充一个条件，使△ADE∽△ACB；
（2）在（1）的条件下，证明△ADE∽△ACB．
分析：（1）由∠A是公共角，且DE与BC不平行，可得当∠ADE=∠C或∠AED=∠B或
=
或AD•AB=AE•AC时，△ADE∽△ACB；
（2）分别利用有两组角对应相等的两个三角形相似与两组对应边的比相等且夹角对应相等的两个三角形相似，即可证得△ADE∽△ACB．
| AD |
| AC |
| AE |
| AB |
（2）分别利用有两组角对应相等的两个三角形相似与两组对应边的比相等且夹角对应相等的两个三角形相似，即可证得△ADE∽△ACB．
解答：解：（1）∵∠A是公共角，且DE与BC不平行，
∴当∠ADE=∠C或∠AED=∠B或
=
或AD•AB=AE•AC时，△ADE∽△ACB；
（2）①∵∠A是公共角，∠ADE=∠C，
∴△ADE∽△ACB．
②∵A是公共角，∠AED=∠B，
∴△ADE∽△ACB．
③∵∠A是公共角，
=
，
∴△ADE∽△ACB．
④∵AD•AB=AE•AC，
∴
=
，
∵∠A是公共角，
∴△ADE∽△ACB．
∴当∠ADE=∠C或∠AED=∠B或
| AD |
| AC |
| AE |
| AB |
（2）①∵∠A是公共角，∠ADE=∠C，
∴△ADE∽△ACB．
②∵A是公共角，∠AED=∠B，
∴△ADE∽△ACB．
③∵∠A是公共角，
| AD |
| AC |
| AE |
| AB |
∴△ADE∽△ACB．
④∵AD•AB=AE•AC，
∴
| AD |
| AC |
| AE |
| AB |
∵∠A是公共角，
∴△ADE∽△ACB．
点评：此题考查了相似三角形的判定与性质．此题难度不大，注意掌握判定定理的应用，注意掌握数形结合思想的应用．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
17、如图，D、E两点分别在AC、AB上，且DE与BC不平行，请填上一个你认为合适的条件：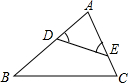
如图，D、E两点分别在AB、AC边上，请填上一个你认为合适的条件，使得△ADE∽△ACB，则这个条件是
如图，A，B两点分别位于一个池塘的两端，小聪想用绳子测量A，B间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达A，B的点C，找到AC，BC的中点M，N，并且测出MN的长为10m，则A，B间的距离为
如图，A、B两点分别位于池塘两侧，小亮用下面的方法测量A、B之间的距离，先在地上取一个可以直接到达A点和B点的C点，连接AC、BC，并分别延长至D、E两点，使DC=AC，EC=BC，那么量出DE的长就是A、B间的距离，请说明一下这样做的道理．
问题解决．