题目内容
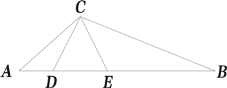
【题目】如图,已知点D、E是△ABC中AB边上的点,△CDE是等边三角形,∠ACB=120°,则下列结论中错误的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
分别证明△ABC∽△ACD、△ABC∽△BCE 、△ACD∽△CEB,运用相似性质即可得出答案.
解:∵△CDE是等边三角形
∴∠CDE=60°
∴∠ADC=120°=∠ACB
又∵∠A=∠A
∴△ABC∽△ACD
∴![]()
∴![]() ,故A选项正确;
,故A选项正确;
∵△CDE是等边三角形
∴∠CED=60°
∴ ∠BEC=120°=∠ACB
又∵∠B=∠B
∴△ABC∽△CBE
∴![]()
∴![]() ,故B选项正确;
,故B选项正确;
∵△CDE是等边三角形
∴∠CDE=60°=∠CED,CD=CE=DE
∴ ∠ADC=120°=∠CEB
又∵△ABC∽△ACD
∴∠ACD=∠B
∴△ACD∽△CBE
∴![]()
又∵ CD=CE=DE
∴![]()
∴![]() ,故C选项正确;
,故C选项正确;
∵△ACE与△BCD不相似,故D选项错误
故选:D

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目