��Ŀ����
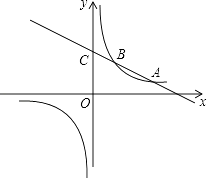
����Ŀ����֪����ABC��ƽ��ֱ������ϵ�е�λ����ͼ����ʾ��A������Ϊ����4��0����B������Ϊ��6��0������DΪAC���е㣬��EΪ�߶�AB��һ���㣬����DE������A��B��C����������ߵĽ���ʽΪy=ax2+bx+8��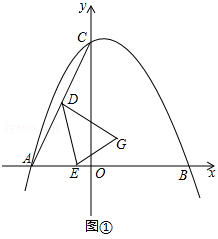
��1���������ߵĽ���ʽ��
��2����ͼ�٣�����ADE��DEΪ�ᷭ�ۣ���A�ĶԳƵ�Ϊ��G������Gǡ�����������ߵĶԳ�����ʱ����G������ꣻ
��3����ͼ�ڣ�����E���߶�AB���˶�ʱ��������y=ax2+bx+8�ĶԳ������Ƿ���ڵ�F��ʹ����C��D��E��FΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����E��F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��������y=ax2+bx+8������A����4��0����B��6��0����
�� ![]() ��
��
��� 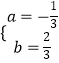 ��
��
�������ߵĽ���ʽ�ǣ�y=�� ![]() x2+
x2+ ![]() x+8
x+8
��2��
�⣺��ͼ1
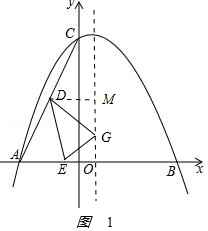 ��
��
��DM�������ߵĶԳ����ڵ�M��
��G�������Ϊ��1��n�����ɷ��۵����ʣ��ɵ�AD=DG��
��A����4��0����C��0��8������DΪAC���е㣬
���D�������ǣ���2��4����
���M�������ǣ�1��4����DM=1������2��=1+2=3��
��B��6��0����C��0��8����
��AC= ![]() =4
=4 ![]() ��
��
��AD=2 ![]() ��
��
��Rt��GDM��DG2=DM2+MG2
32+��4��n��2=20�����n=4 ![]() ��
��
��G���������1��4+ ![]() ����1��4��
����1��4�� ![]() ��
��
��3��
�⣺���ڣ�
C��0��8����D����2��4�������������ĵ�E��F������Ϊ��
����ͼ2
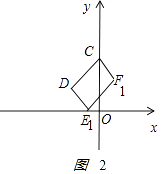 ��
��
CD��EF����CD=EF��CDEFʱ���Խ��ߵĽ��㣨�� ![]() ��4����E1����1��0����F1��1��4����
��4����E1����1��0����F1��1��4����
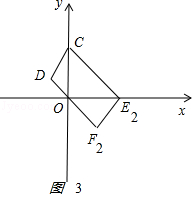
����ͼ3
 ��
��
CD��EF����CD=EF��CDFEʱ���Խ��ߵĽ��㣨 ![]() ��2����E2��3��0����F2��1����4����
��2����E2��3��0����F2��1����4����
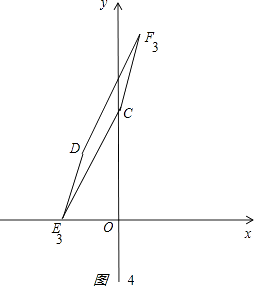
����ͼ4
 ��
��
DE��CF��DE=CF��DECFʱ���Խ��ߵĽ��㣨��1��6����E3����3��0����F3��1��12����
����������E1����1��0����F1��1��4����E2��3��0����F2��1����4����E3����3��0����F3��1��12��
����������1�����ݴ���ϵ�������ɵú�������ʽ����2�������߶��е�����ʣ��ɵ�D�����꣬���ݹ��ɶ������ɵ�AC�ij������ݷ��۵����ʣ��ɵ�DG�ij����ٸ��ݹ��ɶ������ɵ÷��̣����ݽⷽ�̣��ɵô𰸣���3������ƽ���ı��ε����ʣ��ɵô𰸣�
�����㾫�������ù��ɶ����ĸ����ƽ���ı��ε����ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��ֱ֪����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�֣�

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�