Question

已知等腰△ABC中，AB=AC，若AB的垂直平分线与边AC所在直线相交所得锐角为40°，则等腰△ABC的底角∠B的大小为______．

Answer 1

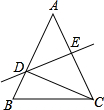
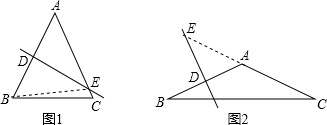
①DE与线段AC相交时，如图1，∵DE是AB的垂直平分线，∠AED=40°，
∴∠A=90°-∠AED=90°-40°=50°，
∵AB=AC，
∴∠ABC=

1

2

（180°-∠A）=

1

2

（180°-50°）=65°；
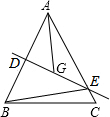
②DE与CA的延长线相交时，如图2，∵DE是AB的垂直平分线，∠AED=40°，
∴∠EAD=90°-∠AED=90°-40°=50°，
∴∠BAC=180°-∠EAD=180°-50°=130°，
∵AB=AC，
∴∠ABC=

1

2

（180°-∠BAC）=

1

2

（180°-130°）=25°，
综上所述，等腰△ABC的底角∠B的大小为65°或25°．
故答案为：65°或25°．