题目内容
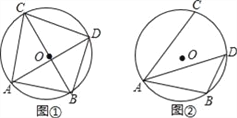
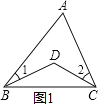
【题目】（1）如图（1），在△ABC中，∠A=62°，∠ABD=20°，∠ACD=35°，求∠BDC的度数．
（2）图（1）所示的图形中，有点像我们常见的学习用品--圆规．我们不妨把这样图形叫做“规形图”，观察“规形图”图（2），试探究∠BDC与∠A、∠B、∠C之间的数量关系，并说明理由．
（3）请你直接利用以上结论，解决以下问题：
①如图（3），把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，若∠A=42°，则∠ABX+∠ACX= °．
②如图（4），DC平分∠ADB，EC平分∠AEB，若∠DAE=60°，∠DBE=140°，求∠DCE的度数．
③如图（5），∠ABD，∠ACD的10等分线相交于点G1、G2…、G9，若∠BDC=140°，∠BG1C=68°，求∠A的度数．
【答案】（1）117°；（2）∠BDC=∠A+∠B+∠C；；（3）①48°；②100°;③60°.
【解析】
（1）先根据三角形内角和定理求出∠ABC+∠ACB的度数，再由∠1=20°，∠2=35°求出∠DBC+∠DCB的度数，由三角形内角和定理即可得出结论；
（2）首先连接AD并延长至点F，然后根据外角的性质，即可判断出∠BDC=∠A+∠B+∠C．
（3）①由（1）可得∠ABX+∠ACX+∠A=∠BXC，然后根据∠A=42°，∠BXC=90°，求出∠ABX+∠ACX的值是多少即可．
②由（1）可得∠DBE=∠DAE+∠ADB+∠AEB，再根据∠DAE=60°，∠DBE=140°，求出∠ADB+∠AEB的值是多少；然后根据∠DCE=
（∠ADB+∠AEB）+∠DAE，求出∠DCE的度数是多少即可．
③根据∠BG1C=
（∠ABD+∠ACD）+∠A，∠BG1C=68°，设∠A为x°，可得∠ABD+∠ACD=140°-x°，解方程，求出x的值，即可判断出∠A的度数是多少．
（1）∵在△ABC中，∠A=62°，
∴∠ABC+∠ACB=180°-62°=118°．
∵∠1=20°，∠2=35°，
∴∠DBC+∠DCB=∠ABC+∠ACB-∠1-∠2=118°-20°-35°=63°．
∴∠BDC=180°-（∠DBC+∠DCB）=180°-63°=117°；
（2）如图2，连接AD并延长至点F，
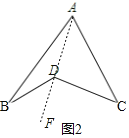
根据外角的性质，可得
∠BDF=∠BAD+∠B，∠CDF=∠C+∠CAD，
又∵∠BDC=∠BDF+∠CDF，∠BAC=∠BAD+∠CAD，
∴∠BDC=∠A+∠B+∠C；
（3）①由（1），可得
∠ABX+∠ACX+∠A=∠BXC，
∵∠A=42°，∠BXC=90°，
∴∠ABX+∠ACX=90°-42°=48°；
故答案为：48°；
②由（1），可得
∠DBE=∠DAE+∠ADB+∠AEB，
∴∠ADB+∠AEB=∠DBE-∠DAE=140°-60°=80°，
∴（∠ADB+∠AEB）=80°÷2=40°，
∴∠DCE=（∠ADB+∠AEB）+∠DAE
=40°+60°
=100°；
③∠BG1C=（∠ABD+∠ACD）+∠A，
∵∠BG1C=68°，
∴设∠A为x°，
∵∠ABD+∠ACD=140°-x°
∴（140-x）+x=70，
∴14-x+x=68，
解得x=60
即∠A的度数为60°．
