Question

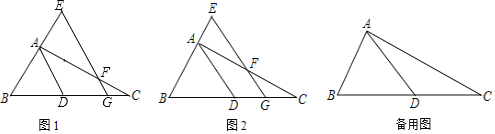
【题目】如图，Rt△ABC中，∠BAC＝90°，AB＝2，AC＝4，D是BC边上一点，且BD＝CD，G是BC边上的一动点，GE∥AD分别交直线AC，AB于F，E两点．

（1）AD＝　 　；

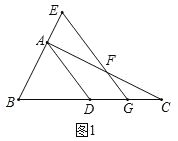
（2）如图1，当GF＝1时，求的值；

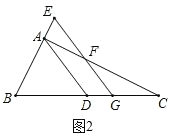
（3）如图2，随点G位置的改变，FG+EG是否为一个定值？如果是，求出这个定值，如果不是，请说明理由．

Answer 1

【答案】（1）AD＝；（2）；（3）FG+EG是一个定值，为 ．

【解析】

（1）先由勾股定理求出BC的长，再由直角三角形斜边中线的性质可求出AD的长；

（2）先证FG=CG=1，通过BD=CDBC=AD，求出BG的长，再证△BGE∽△BDA，利用相似三角形的性质可求出的值；

（3）由（2）知FG=CG，再证EG=BG，即可证FG+EG=BC=2．

（1）∵∠BAC=90°，且BD=CD，

∴ADBC．

∵BC2，

∴AD2．

故答案为：；

（2）如图1．

∵GF∥AD，

∴∠CFG=∠CAD．

∵BD=CDBC=AD，

∴∠CAD=∠C，

∴∠CFG=∠C，

∴CG=FG=1，

∴BG=21．

∵AD∥GE，

∴△BGE∽△BDA，

∴；

（3）如图2，随点G位置的改变，FG+EG是一个定值．理由如下：

∵ADBC=BD，

∴∠B=∠BAD．

∵AD∥EG，

∴∠BAD=∠E，

∴∠B=∠E，

∴EG=BG，

由（2）知，GF=GC，

∴EG+FG=BG+CG=BC=2，

∴FG+EG是一个定值，为2．