Question

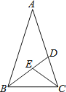
【题目】如图，等腰中，腰，，的平分线交于，的平分线交于．设，则（ ）

A. k2a B. k3a C. D.

Answer 1

【答案】B

【解析】

根据三角形特点，先求出角的度数，从而得到三角形相似，再根据相似三角形对应边成比例即可求得．

：∵AB=AC，∠A=36°
∴∠ABC=∠ACB=72°，
∵BD平分∠ABC，
∴∠ABD=∠DBC=36°，
∵在△ADB中，∠BDC是外角，
∴∠BDC=∠A+∠ABD=72°，
∴AD=BD，BD=BC，
∴△ABC∽△BDC，
∴AB：BC=BC：CD，
同理∠DCE=∠BCE=36°
∴∠DEC=36°+36°=72°，∠BDC=72°
∴△CDE∽△ABC，
∴，

设CD=x，则BD=BC=AD=a-x，
∴，

解得：（舍去），

∴，

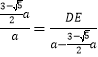解得：DE=,

∵,

∴DE=k3a；
故选：B．