题目内容
【题目】问题引入：
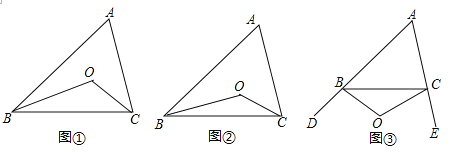
（1）如图①，在△ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A=α，则∠BOC= （用α表示）；如图②，∠CBO=
∠ABC，∠BCO=∠ACB，∠A=α，则∠BOC= （用α表示）
拓展研究：
（2）如图③，∠CBO=∠DBC，∠BCO=∠ECB，∠A=α，请猜想∠BOC= （用α表示），并说明理由．
类比研究：
（3）BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线，它们交于点O，∠CBO=
∠DBC，∠BCO=∠ECB，∠A=α，请猜想∠BOC= ．
【答案】（1）90°+
α，120°+
α；（2）120°-α；（3）
．
【解析】
试题分析：（1）如图①，∵∠ABC与∠ACB的平分线相交于点O，∴∠OBC=∠ABC，∠OCB=∠ACB，∴∠OBC+∠OCB=（∠ABC+∠ACB），在△OBC中，∠BOC=180°﹣（∠OBC+∠OCB）
=180°﹣（∠ABC+∠ACB）=180°﹣（180°﹣∠A）=90°+∠A=90°+α；
如图②，在△OBC中，∠BOC=180°﹣（∠OBC+∠OCB）
=180°﹣（∠ABC+∠ACB）=180°﹣（180°﹣∠A）=120°+∠A=120°+α；
（2）如图③，在△OBC中，∠BOC=180°﹣（∠OBC+∠OCB）
=180°﹣（∠DBC+∠ECB）=180°﹣（∠A+∠ACB+∠A+ABC）=180°﹣（∠A+180°）=120°﹣α；
（3）在△OBC中，∠BOC=180°﹣（∠OBC+∠OCB）
=180°﹣
（∠DBC+∠ECB）=180°﹣（∠A+∠ACB+∠A+ABC）=180°﹣（∠A+180°）
=．
练习册系列答案
相关题目
