题目内容
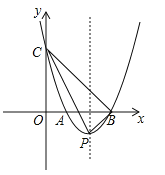
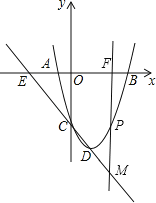
【题目】如图，已知抛物线经过点A（﹣2，0）、B（4，0）、C（0，﹣8）．
（1）求抛物线的解析式及其顶点D的坐标；
（2）直线CD交x轴于点E，过抛物线上在对称轴的右边的点P，作y轴的平行线交x轴于点F，交直线CD于M，使PM=
EF，请求出点P的坐标；
（3）将抛物线沿对称轴平移，要使抛物线与（2）中的线段EM总有交点，那么抛物线向上最多平移多少个单位长度，向下最多平移多少个单位长度．
【答案】（1）
，顶点D的坐标为（1，﹣9）；（2）P（2，﹣8）；（3）抛物线向上最多平移
个单位长度，向下最多平移72个单位长度．
【解析】
试题分析：（1）由于抛物线与x轴的两个交点已知，抛物线的解析式可设成交点式：y=a（x+2）（x﹣4），然后将点C的坐标代入就可求出抛物线的解析式，再将该解析式配成顶点式，即可得到顶点坐标．
（2）先求出直线CD的解析式，再求出点E的坐标，然后设点P的坐标为（m，n），从而可以用m的代数式表示出PM、EF，然后根据PM=
EF建立方程，就可求出m，进而求出点P的坐标．
（3）先求出点M的坐标，然后设平移后的抛物线的解析式为
，然后只需考虑三个临界位置（①向上平移到与直线EM相切的位置，②向下平移到经过点M的位置，③向下平移到经过点E的位置）所对应的c的值，就可以解决问题．
试题解析：（1）根据题意可设抛物线的解析式为y=a（x+2）（x﹣4）．
∵点C（0，﹣8）在抛物线y=a（x+2）（x﹣4）上，∴﹣8a=﹣8，∴a=1，∴y=（x+2）（x﹣4）=
，即
，∴抛物线的解析式为，顶点D的坐标为（1，﹣9）；
（2）如图，设直线CD的解析式为y=kx+b，∴
，解得：
，∴直线CD的解析式为y=﹣x﹣8．当y=0时，﹣x﹣8=0，则有x=﹣8，∴点E的坐标为（﹣8，0）．
设点P的坐标为（m，n），则PM=
=
，EF=m﹣（﹣8）=m+8．
∵PM=EF，∴
．整理得：
，∴（5m+4）（m﹣2）=0，解得：m=
或m=2．∵点P在对称轴x=1的右边，∴m=2．此时，n=
﹣2×2﹣8=﹣8，∴点P的坐标为（2，﹣8）；
（3）当m=2时，y=﹣2﹣8=﹣10，∴点M的坐标为（2，﹣10）．
设平移后的抛物线的解析式为，①若抛物线与直线y=﹣x﹣8相切，则方程
即
有两个相等的实数根，∴1﹣4×1×c=0，∴c=；
②若抛物线经过点M，则有
，∴c=﹣2；
③若抛物线经过点E，则有
，∴c=﹣72．
综上所述：要使抛物线与（2）中的线段EM总有交点，抛物线向上最多平移个单位长度，向下最多平移72个单位长度．
【题目】为了加强对校内外安全监控，创建荔湾平安校园，某学校计划增加15台监控摄像设备，现有甲、乙两种型号的设备，其中每台价格，有效监控半径如表所示，经调查，购买1台甲型设备比购买1台乙型设备多150元，购买2台甲型设备比购买3台乙型设备少400元．
甲型 | 乙型 | |
价格（元/台） | a | b |
有效半径（米/台） | 150 | 100 |
（1）求a、b的值．
（2）若购买该批设备的资金不超过11000元，且两种型号的设备均要至少买一台，学校有哪几种购买方案？
（3）在（2）问的条件下，若要求监控半径覆盖范围不低于1600米，为了节约资金，请你设计一种最省钱的购买方案．
