题目内容
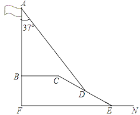
【题目】在学习解直角三角形以后，重庆八中数学兴趣小组测量了旗杆的高度．如图，某一时刻，旗杆AB的影子一部分落在平台上的影长BC为6米，落在斜坡上的影长CD为4米，AB⊥BC，同一时刻，光线与旗杆的夹角为37°，斜坡的坡角为30°，旗杆的高度AB约为（ ）米．（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75， 
≈1.73）
A. 10.61 B. 10.52 C. 9.87 D. 9.37
【答案】A
【解析】
通过作垂线把特殊角放在直角三角形中，利用三角函数由边求边，即由PH求AP，由DQ可求出QH，最后AP+PB=AB求出旗杆高度.
解：如图，过点C作CG⊥EF于点G，延长GH交AD于点H，过点H作HP⊥AB于点P，
则四边形BCHP为矩形，
∴BC=PH=6，BP=CH，∠CHD=∠A=37°，
∴AP= 
=
=8，
过点D作DQ⊥GH于点Q，
∴∠CDQ=∠CEG=30°，
∴CQ= 
CD=2，DQ=CDcos∠CDQ=4×
=2
，
∵QH= 
=
=
，
∴CH=QH﹣CQ=﹣2，
则AB=AP+PB=AP+CH=8+ ﹣2≈10.61，
故答案为：A．
练习册系列答案
相关题目
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
（1）根据表格中的数据，计算出甲的平均成绩是 环，乙的平均成绩是 环；
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加全国比赛更合适，请说明理由．
计算方差的公式：s2＝
[(x1－
)2＋(x2－
)2＋＋(xn－
)2]
