题目内容
如图，正方形ABCD中，E为AB的中点，AF⊥DE于点O，那么
等于（ ）
A．
； B．
； C．
； D．
．
等于（ ）
|
； B．； C．； D．．D
利用△DAO与△DEA相似，对应边成比例即可求解．
解：∠DOA=90°，∠DAE=90°，∠ADE是公共角，∠DAO=∠DEA
∴△DAO∽△DEA
∴
=
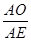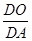
即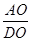
=
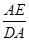
∵AE=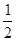
AD
∴=
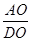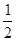
故选D．
本题的关键是利用相似三角形中的相似比，再利用中点和正方形的性质求得它们的比值．
解：∠DOA=90°，∠DAE=90°，∠ADE是公共角，∠DAO=∠DEA
∴△DAO∽△DEA
∴
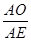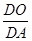
=即
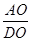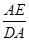
=∵AE=
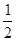AD∴
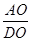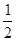
=故选D．
本题的关键是利用相似三角形中的相似比，再利用中点和正方形的性质求得它们的比值．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
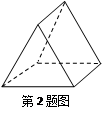
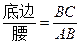.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.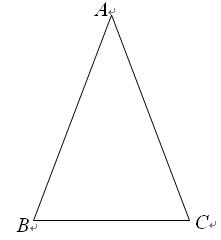
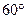的值为（ ）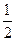
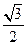
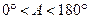，∠A的正对值sad A的取值范围是 .
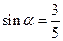，其中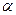
为锐角，试求sad
