题目内容
(本小题满分10分)
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
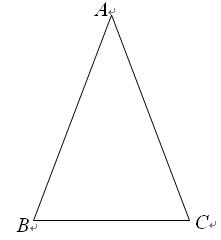
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=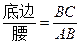 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad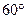 的值为( )
的值为( )
(2)对于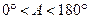 ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .
(3)已知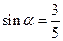 ,其中
,其中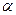 为锐角,试求sad
为锐角,试求sad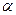 的值.
的值.
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
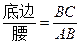 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义,解下列问题:

(1)sad
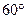 的值为( )
的值为( )A.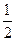 | B.1 | C.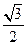 | D.2 |
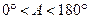 ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .(3)已知
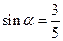 ,其中
,其中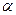 为锐角,试求sad
为锐角,试求sad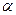 的值.
的值.(1)B; ………………………2分
(2)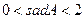 ; ………………………3分
; ………………………3分
(3) 如图,在△ABC中,∠ACB=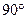 ,sin∠A
,sin∠A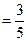 .
.
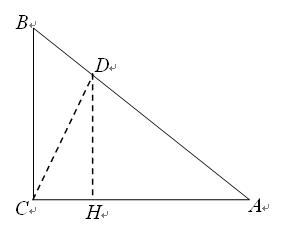
在AB上取点D,使AD=AC,
作DH⊥AC,H为垂足,令BC =3k,AB =5k,
则AD= AC=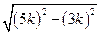 =4k,………………………2分
=4k,………………………2分
又在△ADH中,∠AHD=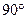 ,sin∠A
,sin∠A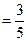 .
.
∴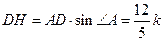 ,
,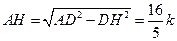 .
.
则在△CDH中,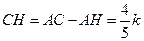 ,
,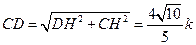 .……………2分
.……………2分
于是在△ACD中,AD= AC=4k,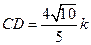 .
.
由正对定义可得:sadA=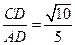 ,即sad
,即sad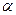
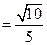 ………………………1分
………………………1分
(2)
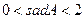 ; ………………………3分
; ………………………3分
(3) 如图,在△ABC中,∠ACB=
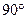 ,sin∠A
,sin∠A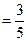 .
.
在AB上取点D,使AD=AC,
作DH⊥AC,H为垂足,令BC =3k,AB =5k,
则AD= AC=
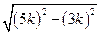 =4k,………………………2分
=4k,………………………2分又在△ADH中,∠AHD=
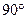 ,sin∠A
,sin∠A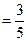 .
.∴
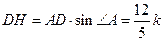 ,
,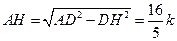 .
.则在△CDH中,
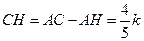 ,
,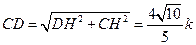 .……………2分
.……………2分于是在△ACD中,AD= AC=4k,
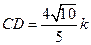 .
.由正对定义可得:sadA=
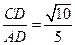 ,即sad
,即sad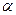
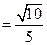 ………………………1分
………………………1分略

练习册系列答案
相关题目
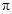 ).
). 的圆;
的圆; 等于( )
等于( )
 ; B.
; B. ; C.
; C. ; D.
; D. .
.