题目内容
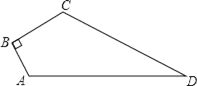
【题目】如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
【答案】36
【解析】
连接AC,由题意可得三角形ABC为直角三角形,由AB与BC的长,利用勾股定理求出AC的长,再由AC,DC及AD的长,利用勾股定理的逆定理得到三角形ADC为直角三角形,分别求出两直角三角形的面积,相加即可得到四边形ABCD的面积.
解:连接AC,

∵∠B=90°,
∴△ABC为直角三角形,
∵BC=4cm,AB=3cm,
∴根据勾股定理得:BD=![]() cm,
cm,
在△ADC中,AC2+DC2=52+122=25+144=169,AD2=132=169,
∵AC2+CD2=AD2,
∴△ACD为直角三角形,
则S四边形ABCD=S△ABC+S△DAC=![]() ABBC+
ABBC+![]() ACCD=
ACCD=![]() ×3×4+
×3×4+![]() ×5×12=6+30=36(cm2).
×5×12=6+30=36(cm2).

练习册系列答案
相关题目