题目内容
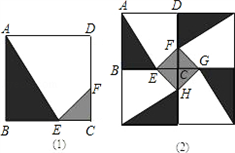
某人定制了一批地砖,每块地砖 (如图1所示)是边长为0.4米的正方形ABCD,点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格之比依次为3:2:1,若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形EFGH。


(1)求证:四边形是正方形;
(2)E,F在什么位置时,定制这批地砖所需的材料费用最省?
(2)E,F在什么位置时,定制这批地砖所需的材料费用最省?
解:(1)图2是由四块图1所示地砖绕点C按顺时针旋转90°后得到,△CFE为等腰直角三角形,
∴四边形EFGH是正方形。
(2)设CE=x,则 ,每块地砖的费用为W,
,每块地砖的费用为W,
制成△CFE、△ABE和四边形AEFD三种材料的每平方米价格依次为3a、2a、a (元),



由a>0,当 时,W有最小值,即总费用为最省
时,W有最小值,即总费用为最省
答:当 米时,总费用最省。
米时,总费用最省。
∴四边形EFGH是正方形。
(2)设CE=x,则
 ,每块地砖的费用为W,
,每块地砖的费用为W,制成△CFE、△ABE和四边形AEFD三种材料的每平方米价格依次为3a、2a、a (元),



由a>0,当
 时,W有最小值,即总费用为最省
时,W有最小值,即总费用为最省答:当
 米时,总费用最省。
米时,总费用最省。
练习册系列答案
相关题目
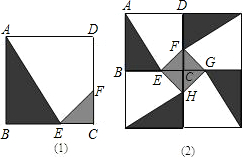 某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.4米的正方形ABCD,点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格依次为30元、20元、10元,若将此种地砖按图(2)所示的形式铺设,且能使中间的阴影部分组成四边形EFGH.
某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.4米的正方形ABCD,点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格依次为30元、20元、10元,若将此种地砖按图(2)所示的形式铺设,且能使中间的阴影部分组成四边形EFGH.