题目内容
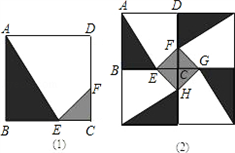
某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.5米的正方形ABCD.点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的价格依次为每平方米30元、20元、10元.若将此种地砖按图(2)所示的形式铺设,则中间的阴影部分组成正方形EFGH.已知烧制该种地砖平均每块需加工费0.35元,若要CE长大于0.1米,且每块地砖的成本价为4元(成本价=材料费用+加工费用),则CE长应为多少米?

解:设CE=x,则BE=0.5-x,由题意得出:CF=CE=x,
∴S△CFE= x2,S△ABE=
x2,S△ABE= ×0.5×(0.5-x),
×0.5×(0.5-x),
S四边形AEFD
=S正方形ABCD-S△CFE-S△ABE
=0.52- x2-
x2- ×0.5×(0.5-x)
×0.5×(0.5-x)
=0.25- x2-
x2- ×0.5×(0.5-x)
×0.5×(0.5-x)
由题意得出:
30× x2-20×
x2-20× ×0.5×(0.5-x)+10×[0.25-
×0.5×(0.5-x)+10×[0.25- x2-
x2- ×0.5×(0.5-x)]+0.35=4,
×0.5×(0.5-x)]+0.35=4,
化简得:10x2-2.5x+0.1=0,
b2-4ac=6.25-4=2.25,
∴x= ,
,
∴x1=0.2,x2=0.05(不合题意舍去).
答:CE的长应为0.2m.
分析:首先表示出S△CFE= x2,S△ABE=
x2,S△ABE= ×0.5×(0.5-x),进而得出S四边形AEFD=S正方形ABCD-S△CFE-S△ABE,即可得出关于x的一元二次方程,求出即可.
×0.5×(0.5-x),进而得出S四边形AEFD=S正方形ABCD-S△CFE-S△ABE,即可得出关于x的一元二次方程,求出即可.
点评:此题主要考查了一元二次方程的应用以及图形面积求法等知识,借助数形结合得出图形面积关系是解题关键.
∴S△CFE=
 x2,S△ABE=
x2,S△ABE= ×0.5×(0.5-x),
×0.5×(0.5-x),S四边形AEFD
=S正方形ABCD-S△CFE-S△ABE
=0.52-
 x2-
x2- ×0.5×(0.5-x)
×0.5×(0.5-x)=0.25-
 x2-
x2- ×0.5×(0.5-x)
×0.5×(0.5-x)由题意得出:
30×
 x2-20×
x2-20× ×0.5×(0.5-x)+10×[0.25-
×0.5×(0.5-x)+10×[0.25- x2-
x2- ×0.5×(0.5-x)]+0.35=4,
×0.5×(0.5-x)]+0.35=4,化简得:10x2-2.5x+0.1=0,
b2-4ac=6.25-4=2.25,
∴x=
 ,
,∴x1=0.2,x2=0.05(不合题意舍去).
答:CE的长应为0.2m.
分析:首先表示出S△CFE=
 x2,S△ABE=
x2,S△ABE= ×0.5×(0.5-x),进而得出S四边形AEFD=S正方形ABCD-S△CFE-S△ABE,即可得出关于x的一元二次方程,求出即可.
×0.5×(0.5-x),进而得出S四边形AEFD=S正方形ABCD-S△CFE-S△ABE,即可得出关于x的一元二次方程,求出即可.点评:此题主要考查了一元二次方程的应用以及图形面积求法等知识,借助数形结合得出图形面积关系是解题关键.

练习册系列答案
相关题目
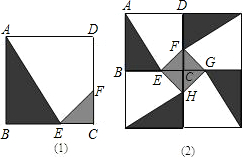 某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.4米的正方形ABCD,点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格依次为30元、20元、10元,若将此种地砖按图(2)所示的形式铺设,且能使中间的阴影部分组成四边形EFGH.
某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.4米的正方形ABCD,点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格依次为30元、20元、10元,若将此种地砖按图(2)所示的形式铺设,且能使中间的阴影部分组成四边形EFGH.