题目内容
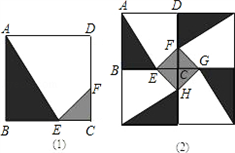
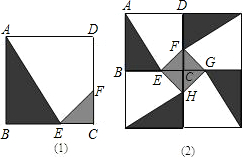 某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.4米的正方形ABCD,点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格依次为30元、20元、10元,若将此种地砖按图(2)所示的形式铺设,且能使中间的阴影部分组成四边形EFGH.
某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.4米的正方形ABCD,点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格依次为30元、20元、10元,若将此种地砖按图(2)所示的形式铺设,且能使中间的阴影部分组成四边形EFGH.(1)判断图(2)中四边形EFGH是何形状,并说明理由;
(2)E、F在什么位置时,定制这批地砖所需的材料费用最省?
分析:(1)图(2)可以看作是由四块图(1)所示地砖绕C点按顺(逆)时针方向旋转90°后得到的,故CE=CF=CG.所以△CEF是等腰直角三角形.因此四边形EFGH是正方形.
(2)费用由三部分的费用组成,因此需求各个部分的面积.因为CE=CF,所以可设CE=x,用含x的式子表示各部分的面积,得出费用的表达式,再运用函数性质解答.
(2)费用由三部分的费用组成,因此需求各个部分的面积.因为CE=CF,所以可设CE=x,用含x的式子表示各部分的面积,得出费用的表达式,再运用函数性质解答.
解答:解:(1)四边形EFGH是正方形.(2分)
图(2)可以看作是由四块图(1)所示地砖绕C点按顺(逆)时针方向旋转90°后得到的,
故CE=CF=CG.
∴△CEF是等腰直角三角形.
∴四边形EFGH是正方形.(4分)
(2)设CE=x,则BE=0.4-x,每块地砖的费用为y,
那么y=
x2×30+
×0.4×(0.4-x)×20+[0.16-
x2-
×0.4×(0.4-x)]×10
=10(x2-0.2x+0.24)
=10[(x-0.1)2+0.23](0<x<0.4).(8分)
当x=0.1时,y有最小值,即费用为最省,此时CE=CF=0.1.
答:当CE=CF=0.1米时,总费用最省.(10分)
图(2)可以看作是由四块图(1)所示地砖绕C点按顺(逆)时针方向旋转90°后得到的,
故CE=CF=CG.
∴△CEF是等腰直角三角形.
∴四边形EFGH是正方形.(4分)
(2)设CE=x,则BE=0.4-x,每块地砖的费用为y,
那么y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=10(x2-0.2x+0.24)
=10[(x-0.1)2+0.23](0<x<0.4).(8分)
当x=0.1时,y有最小值,即费用为最省,此时CE=CF=0.1.
答:当CE=CF=0.1米时,总费用最省.(10分)
点评:此题是数学综合题,涉及四边形和二次函数的有机结合,很有创意.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目