Question

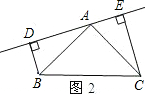
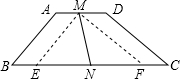
在梯形ABCD中，AD∥BC，M，N分别是边AD，BC的中点，连结MN，已知AD=2，BC=6，若∠B与∠C互余，则MN的长为______．

Answer 1

如图，过点M作ME∥AB，作MF∥CD，
则∠MEF=∠B，∠MFE=∠C，
∵∠B与∠C互余，
∴∠MEF和∠MFE互余，
∴△MEF是直角三角形，且∠EMF=90°，
又∵AD∥BC，
∴四边形ABEM和四边形CDMF是平行四边形，
∴BE=AM，CF=MD，
∴EF=BC-BE-CF=BC-AD=6-2=4，
∵M，N分别是边AD，BC的中点，
∴AM=MD，BN=CN，
∴EN=BN-BE，NF=CN-CF，
∴EN=NF，
∴MN=

1

2

EF=

1

2

×4=2．
故答案为：2．