��Ŀ����
����Ŀ����ͼ��ij�ۿ�Pλ�ڶ�������ĺ������ϡ�Զ�����š������족���ִ�ͬʱ�뿪�ۿڣ�������ͬ�������У���Զ������ÿСʱ����16n mile�������족��ÿСʱ����12n mile�������뿪�ۿ�һ����Сʱ��ֱ�λ�ڵ�Q��R���������30n mile 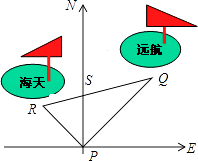
��1����PQ��PR�ij��ȣ�
��2�����֪����Զ�������ض��������У���֪�������족�����ĸ���������
���𰸡�
��1���⣺PQ�ij���16��1.5=24 n mile��
PR�ij���12��1.5=18 n mile��
��2���⣺��RQ2=PR2+PQ2��
���RPQ=90�㣬
�ߡ�Զ�������ض��������У�
�ࡰ���족������������ƫ��45�㣩���У�
����������1������·��=�ٶȡ�ʱ��ֱ����PQ��PR�ij�����2���ٽ�һ�����ݹ��ɶ������涨������֤��������PQR��ֱ�������Σ��Ӷ���⣮

 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�����Ŀ����ѧУ��֯�Ŀ�ѧ���������У�ÿ��μӱ�����������ͬ���ɼ���ΪA��B��C��D�ĸ��ȼ���������Ӧ�ȼ��ĵ÷����μ�Ϊ90�֣�80�֣�70�֣�60�֣�ѧУ�����꼶һ��Ͷ���ijɼ����������Ƴ����µ�ͳ��ͼ��
������������ṩ����Ϣ����������⣺
��1���˴ξ����ж���ɼ���70�ּ������ϵ������� ��
��2����ȫ�±��п�ȱ������ͳ������
ƽ�������֣� | ��λ�����֣� | �������֣� | |
һ�� | 77.6 | 80 | |
���� | 90 |
��3�����������ͼ������ξ����ɼ����з�����д���������ۣ�

