Question

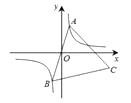
【题目】如图，抛物线y=-x2+(m-1)x+m(m>1)与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C（0,3）.

（1）求抛物线的解析式；
（2）点D和点C关于抛物线的对称轴对称，点F在直线AD上方的抛物线上，FG⊥AD于G，FH//x轴交直线AD于H，求△FGH的周长的最大值；
（3）点M是抛物线的顶点，直线l垂直于直线AM，与坐标轴交于P、Q两点，点R在抛物线的对称轴上，得△PQR是以PQ为斜边的等腰直角三角形，求直线l的解析式.

Answer 1

【答案】
（1）

解：将点C（0,3）代入抛物线y=-x2+(m-1)x+m(m>1)，

得m=3，

则抛物线y=-x2+2x+3.

（2）

解：抛物线y=-x2+2x+3的对称轴为直线x=1,

由点D和点C（0，3）关于抛物线的对称轴对称，

所以D（2,3）.

由抛物线y=-x2+2x+3，令y=0时，-x2+2x+3=0，解得x1=-1,x2=3.

则A（-1,0），B（3,0），

由A（-1,0），D（2,3），设直线AD为y=kx+b,

代入得 ，解得

则直线AD为y=x+1,

则∠DAB=45°，

因为FH//x轴，

所以∠FHG=∠DAB=45°，

又因为FG⊥AD，

所以FG=GH= .

即当FH的长最长时，△FGH的周长的最大值，

设F（x, -x2+2x+3）,则H（-x2+2x+2，-x2+2x+3），

则FH=-x2+2x+2-x=-x2+x+2=-（x- ）2+ ,

当x= 时，FH有最大值为 ，

所以△FGH的周长的最大值为2× × + = + .

（3）

（3）∵抛物线y=-x2+2x+3的顶点坐标为（1，4），

∴直线AM的解析式为y=2x+2，

∵直线l垂直于直线AM，

∴设直线l的解析式为y=- x+b，

∵与坐标轴交于P、Q两点，

∴直线l的解析式为y=- x+b与y轴的交点P（0，b），与x轴的交点Q（2b，0），

设R（1，a），

∴PR2=（-1）2+（a-b）2，QR2=（2b-1）2+a2，PQ2=b2+（2b）2=5b2，

∵△PQR是以PQ为斜边的等腰直角三角形，

∴PR2=QR2，即（-1）2+（a-b）2=QR2=（2b-1）2+a2，

∴-2a=3b-4，①

∴PR2+QR2=PQ2，

即（-1）2+（a-b）2+（2b-1）2+a2=5b2，

∴2a2-2ab-4b+2=0，②

联立①②解得：

，

∴直线l的解析式为y= x+ 或y= x+2．

【解析】（1）抛物线y=-x2+(m-1)x+m(m>1)中只有一个未知数m，则只需要将C（0,3）代入即可求得m；
2）求△FGH的周长的最大值，则不能用轴对称-最短路径的方法；求出A，D的坐标，及直线AD的解析式，可发现∠DAB=45°，根据平行可得∠FHG=∠DAB=45°，则FG=GH= .把求△FGH的周长的最大值，转化成求FH长的最大值，可设F（x, -x2+2x+3）,根据FH//x轴，H在直线AD上得H（-x2+2x+2，-x2+2x+3），写出FH关于x的关系式，并在x的取值范围内，即-1<x<3，求出FH的最大值即可；
3）求得直线AM的解析式为y=2x+2，根据直线l垂直于直线AM，由两条直线垂直可得斜率之积为-1，可设直线l的解析式为y= x+b，得到直线l的解析式为y= x+b与y轴的交点P（0，b），与x轴的交点Q（2b，0），设R（1，a），根据勾股定理及PR=QR列方程即可得到结论．
【考点精析】关于本题考查的二次函数的图象和二次函数的性质，需要了解二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能得出正确答案．