��Ŀ����
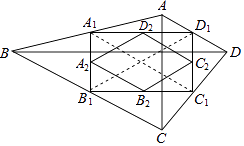
����Ŀ����ͼ���ı���ABCD�У�AC=a��BD=b����AC��BD��˳�������ı���ABCD�����е㣬�õ��ı���A1B1C1D1 �� ��˳�������ı���A1B1C1D1�����е㣬�õ��ı���A2B2C2D2 �� ������˽�����ȥ���õ��ı���AnBnCnDn �� ���н�����ȷ���У� ��
���ı���A2B2C2D2�Ǿ��Σ�
���ı���A4B4C4D4�����Σ�
���ı���A5B5C5D5���ܳ��� ![]() ��
��
���ı���AnBnCnDn������� ![]() ��
��
A.�٢ڢ�
B.�ڢۢ�
C.�٢�
D.�ڢ�
���𰸡�B
���������⣺������A1C1 �� B1D1 �� �����ı���ABCD�У�˳�������ı���ABCD �����е㣬�õ��ı���A1B1C1D1 ��
��A1D1��BD��B1C1��BD��C1D1��AC��A1B1��AC��
��A1D1��B1C1 �� A1B1��C1D1 ��
���ı���A1B1C1D1��ƽ���ı��Σ�
��AC�ABD�����ı���A1B1C1D1�Ǿ��Σ�
��B1D1=A1C1�����ε������Խ�����ȣ���
��A2D2=C2D2=C2B2=B2A2����λ�߶�������
���ı���A2B2C2D2�����Σ�
�ʱ�ѡ������ɢ�֪���ı���A2B2C2D2�����Σ�
�������λ�߶���֪���ı���A4B4C4D4�����Σ�
�ʱ�ѡ����ȷ���۸�����λ�ߵ�������֪��A5B5= ![]() A3B3=
A3B3= ![]() A1B1=
A1B1= ![]() AC��B5C5=
AC��B5C5= ![]() B3C3=
B3C3= ![]() B1C1=
B1C1= ![]() BD��
BD��
���ı���A5B5C5D5���ܳ���2�� ![]() ��a+b��=
��a+b��= ![]() ��
��
�ʱ�ѡ����ȷ���ܡ��ı���ABCD�У�AC=a��BD=b����AC�ABD��
��S�ı���ABCD=ab��2��
�������ε���λ�ߵ����ʿ�����֪��ÿ�õ�һ���ı��Σ����������Ϊԭ����һ�룬
�ı���AnBnCnDn������� ![]() ��
��
�ʱ�ѡ����ȷ��
�����������ڢۢ���ȷ��
��ѡ��B��