题目内容
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
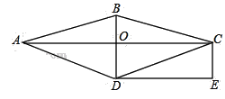
(1)求证:四边形OCED是矩形;(2)若CE=1,DE=2,求菱形ABCD的面积。
【答案】(1)见解析;(2)S菱形ABCD=4.
【解析】
(1)要证明四边形OCED是矩形,只需推知四边形OCED是平行四边形,且有一内角为90度即可;
(2)由菱形的对角线互相垂直平分和菱形的面积公式解答.
解:(1)证明:∵CE//BD,DE//AC
∴四边形ODEC为平行四边形
∵四边形ABCD是菱形
∴AC⊥BD
∴∠COD=90°
∴四边形ODEC为矩形.
(2)由(1)知,平行四边形OCED是矩形,则CE=OD=1,DE=OC=2.
∵四边形ABCD是菱形,
∴AC=2OC=4,BD=2OD=2,
∴菱形ABCD的面积为:![]() ACBD=
ACBD=![]() ×4×2=4.
×4×2=4.

练习册系列答案
相关题目
【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
第x天 | 1≤x≤6 | 6<x≤15 |
每天的销售量y/盒 | 10 | x+6 |
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.