题目内容
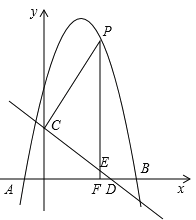
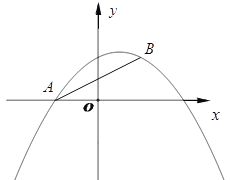
【题目】如图,已知抛物线![]() 经过
经过![]() 、
、![]() 两点,
两点,
(1)求抛物线的解析式;
(2)阅读理解:在同一平面直角坐标系中,直线![]() (
(![]() 、
、![]() 为常数,且
为常数,且![]() ),直线
),直线![]() (
(![]() 、
、![]() 为常数,且
为常数,且![]() ),若
),若![]() ,则
,则![]() .
.
解决问题:①若直线![]() 与直线
与直线![]() 互相垂直,求
互相垂直,求![]() 的值;
的值;
②在抛物线上是否存在点![]() ,使得△PAB是以
,使得△PAB是以![]() 为直角边的直角三角形?若存在,请求出点
为直角边的直角三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)点![]() 是抛物线上一动点,且在直线
是抛物线上一动点,且在直线![]() 的上方(不与
的上方(不与![]() 、
、![]() 重合),求点
重合),求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
【答案】(1) y=-![]() x2+
x2+![]() x+1;(2)① -
x+1;(2)① -![]() ;②存在,点P的坐标(6,-14)或(4,-5);(3)
;②存在,点P的坐标(6,-14)或(4,-5);(3)![]() .
.
【解析】
(1)根据待定系数法,可得函数解析式;
(2)①利用垂线间的关系![]() ,即可求出m的值;
,即可求出m的值;
②分两种情况:当PA⊥AB时;当PB⊥AB时。根据垂线间的关系,可得PA,PB的解析式,根据解方程组,可得P点坐标;
(3)作MQ⊥x轴交AB于Q。设M的横坐标为t,根据垂直于x轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,用t表示出MQ,于是可表示出三角形ABM的面积,是一个二次函数,根据二次函数的性质,可得面积的最大值,根据三角形的底一定时面积与高成正比,可得三角形高的最大值.
解:(1)将A,B点坐标代入,得
![]() ,
,
解得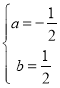 ,
,
所以抛物线的解析式为![]() ;
;
(2)①由直线y=2x-1与直线y=mx+2互相垂直,得
2m=-1,
即![]() ;
;
故答案为:![]() ;
;
②AB的解析式为![]() ,
,
当PA⊥AB时,PA的解析式为y=-2x-2,
联立PA与抛物线,得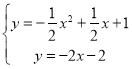 ,
,
解得![]() (舍),
(舍),![]() ,
,
即P(6,-14);
当PB⊥AB时,PB的解析式为y=-2x+3,
联立PB与抛物线,得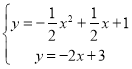 ,
,
解得![]() (舍去),
(舍去),![]() ,
,
即P(4,-5),
综上所述:△PAB是以AB为直角边的直角三角形,点P的坐标为(6,-14)(4,-5);
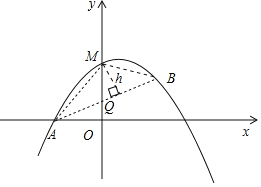
(3)如图:作MQ⊥x轴交AB于Q。
 ,
,
![]() ,
,
![]()
S△MAB=![]() MQ|xB-xA|
MQ|xB-xA|
![]()
=![]() ,
,
![]() 当t=0时,S取最大值
当t=0时,S取最大值![]() ,即M(0,1).
,即M(0,1).
由勾股定理,得
![]() ,
,
设M到AB的距离为h,由三角形的面积,得
![]()
点M到直线AB的距离的最大值是![]() .
.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
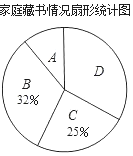
口算与应用题卡系列答案【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.