题目内容
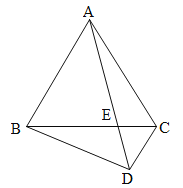
【题目】已知:如图,△ABC 是等边三角形,AB=4,E 是BC 边上任意一点(不与B、C重合),在三角形外作等边△CDE,连结AE、BD.
(1)根据题意画出图形;
(2)求证:AE=BD;
(3)△BDC能否为直角三角形?若能,求出BD长;若不能,请说明理由.
【答案】(1)见解析;(2)见解析;(3)能,BD=![]()
【解析】
(1)根据题意画出图形即可;
(2)根据SAS证明△ACE≌△BCD即可;
(3)当∠CBD=30°时,△BDC为直角三角形,再根据勾股定理可求出BD的长.
解:(1)如图所示;
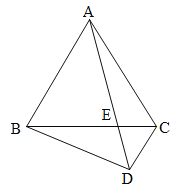
(2)证明:∵△ABC,△CDE 是等边三角形,
∴AC=BC,CE=CD,∠ACE=∠BCD=60°,
在△ACE和△BCD中
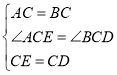
∴△ACE≌△BCD
∴AE=BD;
(3)能.
由已知和(2)可得,当∠CBD=30°时,△BDC为直角三角形
此时在Rt△BDC中,∠CBD=30°,BC=AB=4
∴CD=2
∴BD=![]() =
=![]()

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目