题目内容
如图,在半径为5的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为 ; 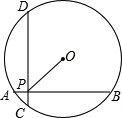
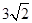
解析试题分析:作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,由垂径定理、勾股定理得:OM=ON=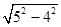 =3,∵弦AB、CD互相垂直,∴∠DPB=90°,∵OM⊥AB于M,ON⊥CD于N,∴∠OMP=∠ONP=90°,∴四边形MONP是正方形,∴OP=
=3,∵弦AB、CD互相垂直,∴∠DPB=90°,∵OM⊥AB于M,ON⊥CD于N,∴∠OMP=∠ONP=90°,∴四边形MONP是正方形,∴OP=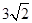
考点:勾股定理
点评:该题主要考查学生勾股定理的应用,结合了圆,以及弦的用法,需要学生灵活变动。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
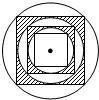 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
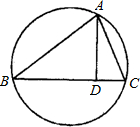 如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为
如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为 如图,在半径为6cm的圆中,弦AB长6
如图,在半径为6cm的圆中,弦AB长6 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是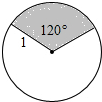 如图,在半径为1的圆中,圆心角为120°的扇形AOB的面积等于
如图,在半径为1的圆中,圆心角为120°的扇形AOB的面积等于