题目内容
【题目】在平面直角坐标系xOy中,将点![]() 定义为点
定义为点![]() 的“关联点”. 已知点
的“关联点”. 已知点![]() 在函数
在函数![]() 的图像上,将点A的“关联点”记为点
的图像上,将点A的“关联点”记为点![]() .
.
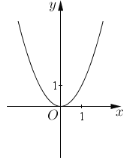
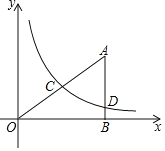
(1)请在如图基础上画出函数![]() 的图像,简要说明画图方法;
的图像,简要说明画图方法;
(2)如果点![]() 在函数
在函数![]() 的图像上,求点
的图像上,求点![]() 的坐标;
的坐标;
(3)将点![]() 称为点
称为点![]() 的“待定关联点”(其中
的“待定关联点”(其中![]() ),如果点
),如果点![]() 的“待定关联点”
的“待定关联点”![]() 在函数
在函数![]() 的图像上,试用含
的图像上,试用含![]() 的代数式表示点
的代数式表示点![]() 的坐标.
的坐标.
【答案】(1)见解析,将图中的抛物线![]() 向下平移2个单位长,可得抛物线
向下平移2个单位长,可得抛物线![]() ;(2)(2,2);(3)
;(2)(2,2);(3)![]()
【解析】
(1)利用图像的平移规律,将![]() 向下平移2个单位长度即可得到
向下平移2个单位长度即可得到![]()
(2)先根据题意求出![]() ,再代入到
,再代入到![]() 中,联合A代入到
中,联合A代入到![]() 即可求出答案.
即可求出答案.
(3)将![]() 代入
代入![]() 中解出x的值,可点
中解出x的值,可点![]() 的坐标即可用含n的代数式表示.
的坐标即可用含n的代数式表示.
如图
将图9中的抛物线![]() 向下平移2个单位长,可得抛物线
向下平移2个单位长,可得抛物线![]()
画法:①列表;②描点(五点画图法);③用光滑的曲线连接这五个点.
(2)由题意,得点![]() 的“关联点”为
的“关联点”为![]()
由点![]() 在抛物线
在抛物线![]() 上,可得
上,可得![]() ,
,![]()
又∵![]() 在抛物线
在抛物线![]() 上,∴
上,∴![]()
解得![]() .将
.将![]() 代入
代入![]() ,得
,得![]()
(3)点![]() 的“待定关联点”为
的“待定关联点”为![]() ,
,
∵![]() 在抛物线
在抛物线![]() 的图像上,∴
的图像上,∴![]() .
.
∴![]() ,
,![]() .又∵
.又∵![]() ,∴
,∴![]() .
.
当![]() 时,
时,![]() ,故可得
,故可得![]() .
.

【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .