题目内容
【题目】如图,一渔船自西向东追赶鱼群,在A处测得某无名小岛C在北偏东60°方向上,前进2nmile到达点B处,此时测得无名小岛C在东北方向上.已知无名小岛周围2.5nmile内有暗礁.问:渔船继续追赶鱼群有无触礁危险?
(参考数据:
≈1.414,
≈1.732)
【答案】渔船继续追赶鱼群没有触礁危险.
【解析】分析：根据题意可知，实质是比较C点到AB的距离与10的大小．因此作CD⊥AB于D点，求CD的长．
详解：如图,过点C作CD⊥AB的延长线于点D,设CD=x,
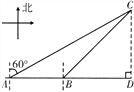
则∠CDA=90°.
在Rt△BDC中,
∵∠CBD=45°,
∴∠BCD=90°-∠CBD=90°-45°=45°,
∴∠BCD=∠CBD,
∴BD=CD=xnmile.
在Rt△ADC中,
∵∠CAD=30°,
∴tan∠CAD=
,
即tan30°=
,
解得AD=
x.
∵AB=2,∴AD-BD=2,∴x-x=2,解得x=+1.
∴CD=+1≈1.732+1=2.732>2.5,
∴渔船继续追赶鱼群没有触礁危险.
【题目】在高处让一物体由静止开始落下，它下落的路程s与时间t之间的关系如下表：
时间t(秒) | 1 | 2 | 3 | 4 | 5 |
落下路程s(米) | 4.9×1 | 4.9×4 | 4.9×9 | 4.9×16 | 4.9×25 |
（1）请根据表格中的数据写出时间t与物体落下的路程s之间的关系；
（2）算出当t=4.5秒时，物体落下的路程.
【题目】某超市第一次用12000元购进甲、乙两种商品.其中乙商品的件数比甲商品件数的
倍多15件，甲、乙两种商品的进价和售价如下表：
甲 | 乙 | |
进价（元件） | 44 | 60 |
售价（元件） | 58 | 80 |
（1）该超市第一次购进甲、乙两种商品各多少件？
（2）该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？
（3）该超市第二次以第一次的进价又购进甲、乙两种商品，其中甲商品的件数不变，乙商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多360元，求第二次乙商品是按原价打几折销售？（提示：设原价打
折销售，则实际售价=原价
）
