题目内容
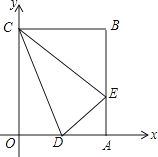
【题目】如图，在矩形OABC中，OA=3，OC=2，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数y= 
（k＞0）的图象与BC边交于点E．
（1）当F为AB的中点时，求该函数的解析式；
（2）当k为何值时，△EFA的面积最大，最大面积是多少？
【答案】
（1）
解：∵在矩形OABC中，OA=3，OC=2，
∴B（3，2），
∵F为AB的中点，
∴F（3，1），
∵点F在反比例函数y= 
（k＞0）的图象上，
∴k=3，
∴该函数的解析式为y= 
（x＞0）
（2）
解：由题意知E，F两点坐标分别为E（ 
，2），F（3， 
），
∴S△EFA= 
AFBE= × 
k（3﹣ k），
= k﹣ 
k2
=﹣ （k2﹣6k+9﹣9）
=﹣ （k﹣3）2+ 
当k=3时，S有最大值．
S最大值=
【解析】（1）当F为AB的中点时，点F的坐标为（3，1），由此代入求得函数解析式即可；（2）根据图中的点的坐标表示出三角形的面积，得到关于k的二次函数，利用二次函数求出最值即可．此题属于反比例函数综合题，涉及的知识有：坐标与图形性质，待定系数法确定反比例解析式，以及二次函数的性质，熟练掌握待定系数法是解本题的关键．
【考点精析】认真审题，首先需要了解二次函数的最值(如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a)．
练习册系列答案
相关题目
