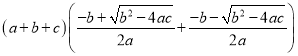题目内容
【题目】阅读下面材料：小科遇到这样一个问题：如图1，△ABC是等边三角形，点P是三角形内部一点，且PA＝3，PB＝4，PC＝5，求∠APB的度数．
小科是这样思考的：如图2，将AP绕着点A逆时针旋转60°得到AP′，连接P′C，P′P，可以根据边角边证明△APB≌△AP′C，进而通过判定得到两个特殊的三角形，解决问题．
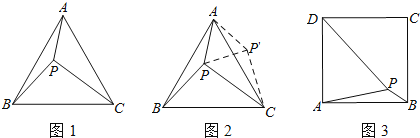
（1）小科遇到的问题中，∠APB的度数是 ；（请直接写出答案）
参考小科同学的思路，解决下列问题：
（2）如图3，在正方形ABCD内有一点P，且PA＝2
，PB＝2，PD＝2
，
①求∠APB的度数；②求正方形的边长
【答案】（1）150°；（2）①135°；②
.
【解析】
（1）把△APB绕点A逆时针旋转60°得到△ACP′，由旋转的性质可得P′A=PA，P′C=PB，∠PAP′=60°，证出△APP′是等边三角形，由等边三角形的性质求出PP′=PA=3，∠AP′P=60°，再由勾股定理逆定理求出∠PP′C=90°，求出∠AP′C，即为∠APB的度数；
（2）①把△APB绕点A逆时针旋转90°得到△ADP′，由旋转的性质可得P′A=PA，P′D=PB，∠PAP′=90°，证出△APP′是等腰直角三角形，由等腰直角三角形的性质求出PP′，∠AP′P=45°，再利用勾股定理逆定理求出∠PP′D=90°，然后求出∠AP′D，即为∠APB的度数；
②求出点P′、P、B三点共线，过点A作AE⊥PP′于E，根据等腰直角三角形的性质求出AE=PE=
PP′，然后求出BE，在Rt△ABE中，利用勾股定理求出AB即可．
解：（1）如图2，把△APB绕点A逆时针旋转60°得到△ACP′，
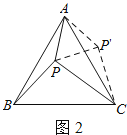
由旋转的性质，P′A=PA=3，P′D=PB=4，∠PAP′=60°，∠APB=∠AP′C，
∴△APP′是等边三角形，
∴PP′=PA=3，∠AP′P=60°，
∵PP′2+P′C2=32+42=25，PC2=52=25，
∴PP′2+P′C2=PC2，
∴∠PP′C=90°，
∴∠AP′C=∠AP′P+∠PP′C=60°+90°=150°；
故∠APB=∠AP′C=150°；
故答案为：150°．
（2）①如图3，把△APB绕点A逆时针旋转90°得到△ADP′，
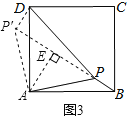
由旋转的性质，P′A=PA=2
，P′D=PB=2，∠PAP′=90°，
∴△APP′是等腰直角三角形，
∴PP′=PA=4，∠AP′P=45°，
∵PP′2+P′D2=42+22=20，PD2=
，
∴PP′2+P′D2=PD2，
∴∠PP′D=90°，
∴∠AP′D=∠AP′P+∠PP′D=45°+90°=135°，
故∠APB=∠AP′D=135°，
②∵∠APB+∠APP′=135°+45°=180°，
∴点P′、P、B三点共线，
过点A作AE⊥PP′于E，
则AE=PE=PP′=×4=2，
∴BE=PE+PB=2+2=4，
在Rt△ABE中，AB=
∴正方形的边长为.
