题目内容
【题目】如图,在平面直角坐标系中,点A的坐标为(6,0),点B的坐标为(0,2),点M从点A出发沿x轴负方向以每秒3cm的速度移动,同时点N从原点出发沿y轴正方向以每秒1cm的速度移动.设移动的时间为t秒.
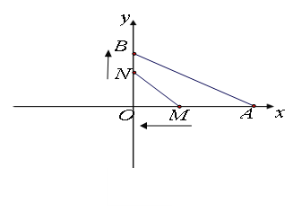
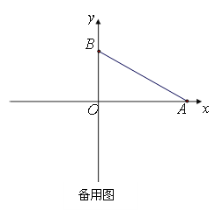
(1)若点M在线段OA上,试问当t为何值时,△ABO与以点O、M、N为顶点的三角形相似?
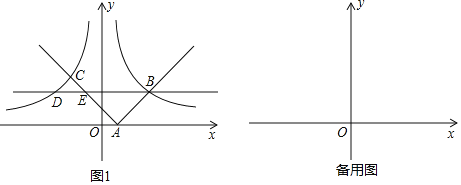
(2)若直线y=x与△OMN外接圆的另一个交点是点C.
①试说明:当0<t<2时,OM、ON、OC在移动过程满足OM+ON=![]() OC;
OC;
②试探究:当t>2时,OM、ON、OC之间的数量关系是否发生变化,并说明理由.
【答案】(1)当t为1或1.8时,△ABO与以点O、M、N为顶点的三角形相似;(2)①说明见解析;②ON-OM=![]() OC,理由见解析.
OC,理由见解析.
【解析】
(1)根据题意先把OA、OB的值算出来,再根据相似三角形的性质列出等量关系式,即可把时间t算出来.
(2) ①在ON的延长线的截取ND=OM,证CN=CM并且△CND≌△CMO,接着把∠COD的度数算出来,即可证明OM+ON=![]() OC;
OC;
②先证△CDO为等腰直角三角形,再证明△CDN≌△COM即可得到.
(1)由题意,得OA=6,OB=2.
当0<t<2时,OM=6-3t,ON=t.
若△ABO∽△MNO,则![]() ,即
,即![]() .解得t=1.
.解得t=1.
若△ABO∽△NMO,则![]() ,即
,即![]() .解得t=1.8.
.解得t=1.8.
综上,当t为1或1.8时,△ABO与以点O、M、N为顶点的三角形相似.
(2)①当0<t<2时,在ON的延长线的截取ND=OM.
∵直线y=x与x轴的夹角为![]() ,∴OC平分∠AOB.
,∴OC平分∠AOB.
∴∠AOC=∠BOB.
∴![]() .
.
∴CN=CM.
又∵ 在⊙O中∠CNO+∠CMO=180°,∠DNC+∠CNO=180°,
∴∠CND=∠CMO.
∴△CND≌△CMO.
∴CD=CO,∠DCN=∠OCM.
又∵∠AOB=90°,∴MN为⊙O的直径.
∴∠MCN=90°.
∴∠OCM+∠OCN=90°.
∴∠DCN+∠OCN=90°.
∴∠OCD=90°,
又∵CD=CO,∴OD=![]() OC.
OC.
∴ON+ND=![]() OC,
OC,
∴OM+ON=![]() OC.
OC.

②当 t >2时,ON-OM=![]() OC.
OC.
过点C作CD⊥OC交ON于点D.
∵∠COD=45°,
∴△CDO为等腰直角三角形,
∴OD=![]() OC,
OC,
连接MC,NC,
∵MN为⊙O的直径,∴∠MCN=90°,
又∵在⊙O中,∠CMN=∠CNM=45°,∴MC=NC,
又∵∠OCD=∠MCN=90°,∴∠DCN=∠OCM,
∴△CDN≌△COM.∴DN=OM,
又∵OD=![]() OC.,∴ON-DN=
OC.,∴ON-DN=![]() OC,
OC,
∴ON-OM=![]() OC.
OC.

【题目】观察下面的表格,根据表格解答下列问题:
| -2 | 0 | 1 |
| 1 | ||
| -3 | -3 |
(1)写出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)在直角坐标系中画出二次函数![]() 的图象;并根据图象写出使不等式
的图象;并根据图象写出使不等式![]() 成立时
成立时![]() 的取值范围;
的取值范围;
(3)设该图象与![]() 轴两个交点分别为
轴两个交点分别为![]() ,
,![]() ,与
,与![]() 轴交点为
轴交点为![]() ,直接写出
,直接写出![]() 的外心坐标.
的外心坐标.