题目内容
【题目】观察下面的表格,根据表格解答下列问题:
| -2 | 0 | 1 |
| 1 | ||
| -3 | -3 |
(1)写出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)在直角坐标系中画出二次函数![]() 的图象;并根据图象写出使不等式
的图象;并根据图象写出使不等式![]() 成立时
成立时![]() 的取值范围;
的取值范围;
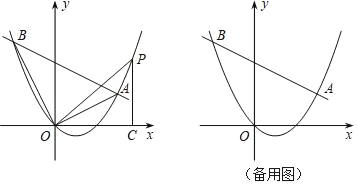
(3)设该图象与![]() 轴两个交点分别为
轴两个交点分别为![]() ,
,![]() ,与
,与![]() 轴交点为
轴交点为![]() ,直接写出
,直接写出![]() 的外心坐标.
的外心坐标.

【答案】(1)![]() ,
,![]() ,
,![]() ;(2)图见解析,
;(2)图见解析,![]() ;(3)外心坐标是
;(3)外心坐标是![]()
【解析】
(1)分析表格,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,建立方程解出
,建立方程解出![]() 即可;(2)根据(1)中的函数解析式求出函数图象与坐标轴的交点坐标画出函数图象;根据函数图象求出
即可;(2)根据(1)中的函数解析式求出函数图象与坐标轴的交点坐标画出函数图象;根据函数图象求出![]() 时
时![]() 的取值范围; (3)
的取值范围; (3)![]() 的外心为三边中垂线的交点,求交点坐标即可.
的外心为三边中垂线的交点,求交点坐标即可.
(1)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,建立方程:
,建立方程:
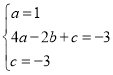 解得:
解得: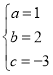
∴![]() ,
,![]() ,
,![]() ;
;
(2)由(1)知:函数解析式为![]() 令
令![]() 可得函数与
可得函数与![]() 轴的交点坐标为
轴的交点坐标为![]() ,函数与
,函数与![]() 轴的交点坐标为
轴的交点坐标为![]() ,根据三个点,画出如图:
,根据三个点,画出如图:
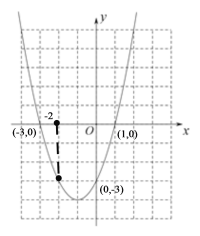
观察图象:当时![]()
![]() 的取值范围是
的取值范围是![]()
(3三角形的外心为三边垂直平分线的交点,如图![]() 为
为![]() 的中垂线与
的中垂线与![]() 的中垂线交点:
的中垂线交点:
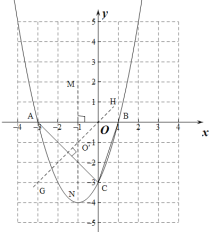
![]() 的中垂线为
的中垂线为![]() ,设
,设![]() 的直线解析式为
的直线解析式为![]() ,代
,代![]()
得:![]() 解得
解得![]()
∴![]() 的直线解析式为
的直线解析式为![]()
∴设![]() 的中垂线
的中垂线![]() 解析式为:
解析式为:![]()
∵![]() 中点为
中点为![]() 代入:
代入:
∴EF的解析式为![]()
联立解方程:![]()
∴外心坐标![]() .
.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案【题目】近日,全省各地市的2019年初中毕业升学体育考试工作正依照某省教育厅的具体要求在有条不紊的进行当中,某中学在正式考试前,为了让同学们在中招体育考试中获得理想成绩,同时为了了解学生的当前水平,按批次进行了模拟考试,并随机抽取若干名学生问卷调查,现将调查结果绘制成如下不完整的统计图表:
组别 | 成绩范围x(分) | 频数(人数) |
A | 60<x≤70 | 54 |
B | 50<x≤60 | m |
C | 40<x≤50 | n |
D | 30<x≤40 | 6 |
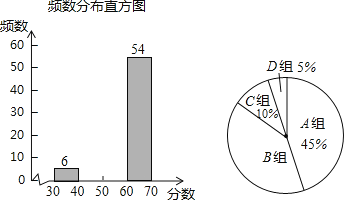
(1)这次调查的总人数有 人,表中的m= ,n= ;
(2)扇形统计图中B组对应的圆心角为 °;
(3)请补全频数分布直方图;
(4)若该校九年级共有学生2700名,且都参加了正式的初中毕业升学体育考试,小华也参加了这次考试并得了67分,若规定60分以上为优秀,体育老师想要在获得优秀的学生中随机抽出1名,作为学生代表向学弟学妹们传授经验,求抽到小华的概率.