题目内容
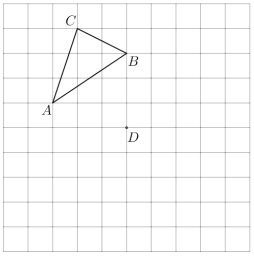
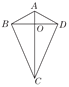
【题目】两组邻边分别相等的四边形我们称它为筝形．如图，在四边形ABCD中，AB＝AD，BC＝DC，AC与BD相交于点O，下列判断正确的有_____(填序号)．
①AC⊥BD；②AC，BD互相平分；③AC平分∠BCD；④∠ABC＝∠ADC＝90°；⑤筝形ABCD的面积为
AC·BD.
【答案】①③⑤
【解析】
根据题意AB=AD，BC=DC，AC与BD相交于点O可以证明△ABC≌△ADC、△ABO≌△ADO，可得AC、BD互相垂直，AC平分∠BAD、∠BCD．
∵在△ABC与△ADC中，
，∴△ABC≌△ADC（SSS），∴∠BAO=∠DAO，∠BCO=∠DCO，即AC平分∠BCD．故③正确；
∵AC平分∠BAD、∠BCD，△ABD与△BCD均为等腰三角形，∴AC、BD互相垂直，但不平分．故①正确，②错误；
由题中条件无法证明∠ABC=∠ADC=90°，故④错误；
∵AC、BD互相垂直，∴筝形ABCD的面积为：
ACBO
ACOD
ACBD．
故⑤正确；
综上所述：正确的说法是①③⑤．
故答案为：①③⑤．
练习册系列答案
相关题目
【题目】某商场为了迎接“6.1儿童节“，以调低价格的方式促销n个不同的玩具，调整后的单价y（元）与调整前的单价x（元）满足一次函数关系，如表：
第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
调整前单价x （元） | x1 | x2=6 | x3=72 | x4 | … | xn |
调整后单价y （元） | y1 | y2=4 | y3=59 | y4 | … | yn |
当这些玩具调整后的单价都大于2元时，解答下列问题：
（1）y与x的函数关系式为，x的取值范围为；
（2）某个玩具调整前单价是108元，顾客购买这个玩具省了元；
（3）这n个玩具调整前、后的平均单价分别为 
（元）、 
（元），猜想 与 的关系式，并写出推导过程．
