题目内容
【题目】如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
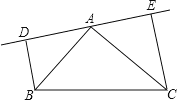
(1)如图1,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线.
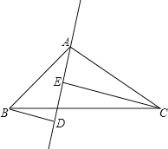
(2)如图2,已知△ABC是特异三角形,且∠A=30°,∠B为钝角,求出所有可能的∠B的度数.
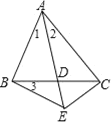
(3)如图3,△ABC是一个腰长为2的等腰锐角三角形,且它是特异三角形,若它的顶角度数为整数,请求出其特异线的长度;若它的顶角度数不是整数,请直接写出顶角度数.
【答案】
(1)解:证明:如图1中,
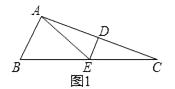
∵DE是线段AC的垂直平分线,
∴EA=EC,即△EAC是等腰三角形,
∴∠EAC=∠C,
∴∠AEB=∠EAC+∠C=2∠C,
∵∠B=2∠C,
∴∠AEB=∠B,即△EAB是等腰三角形,
∴AE是△ABC是一条特异线
(2)解:如图2中,
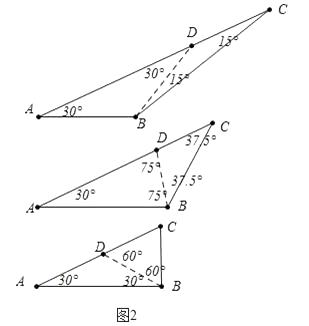
当BD是特异线时,如果AB=BD=DC,则∠ABC=∠ABD+∠DBC=120°=15°=135°,
如果AD=AC,DB=DC,则∠ABC=∠ABD+∠DBC=75°+37.5°=112.5°,
如果AD=DB,DC=DB,则ABC=∠ABD+∠DBC=30°+60°=90°(不合题意舍弃).
如图3中,当AD是特异线时,AB=BD,AD=DC,则∠ABC=180°﹣20°﹣20°=140°
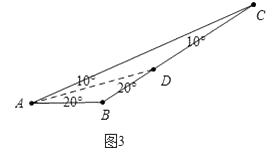
当CD为特异线时,不合题意.
∴符合条件的∠ABC的度数为135°或112.5°或140°
(3)解:如图3中,
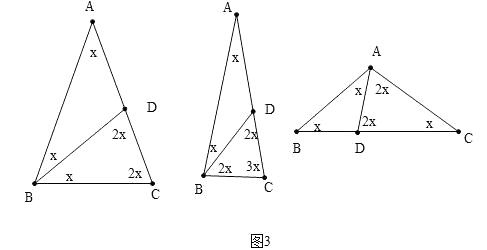
当BD是特异线时,有两种情形,如果AD=BD=BC,设∠A=x,则x+2x+2x=180°,解得x=36°,
设AD=BD=BC=a,
由△BCD∽△ABC得到 ![]() ,
,
∴ ![]() ,
,
∴a2+2a﹣4=0,
∴a=﹣1+ ![]() 或﹣1﹣
或﹣1﹣ ![]() (舍弃).
(舍弃).
如果AD=BC,BC=CD,设∠A=x,则2x+2x+3x=180°解得x=( ![]() )°.
)°.
当AD是特异线时,如果DA=DB,CA=CD,设∠B=∠C=x,则x+2x+2x=180°,解得x=36°,
∴∠BAC=108°,不符合题意.
∴△ABC是一个腰长为2的等腰锐角三角形,且它是特异三角形,若它的顶角度数为整数,其特异线的长度为﹣1+ ![]() ,
,
若它的顶角度数不是整数,则顶角度数为( ![]() )°
)°
【解析】(1)由DE是线段AC的垂直平分线,易得△EAC是等腰三角形;又∠B=2∠C,利用外角关系易得∠AEB=∠B,即△EAB是等腰三角形,特异线可证。
(2)由△ABC是特异三角形,且∠A=30°,易得若∠A分别为等腰三角形的顶角时,以及∠A为底角时∠ADB,∠ABD为顶角的情况,可能符合题意;还要考虑AD为特异线的情况;最后要注意检验∠B是否为钝角,可得最后结果
(3)当BD是特异线时,有两种情形,如果AD=BD=BC则可以利用相似可得a的结果,如果AD=BC,BC=CD解得顶角为分数,不用计算a
若当AD是特异线时,如果DA=DB,CA=CD算得顶角为钝角,不符合要求,舍去。最后总结两种结果。