题目内容
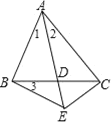
【题目】已知,如图,在△ABC中,D为BC边上的一点,延长AD到点E,连接BE、CE,
∠ABD+![]() ∠3=90°,∠1=∠2=∠3,下列结论:①△ABD为等腰三角形;②AE=AC;③BE=CE=CD;④CB平分∠ACE.其中正确的结论个数有( )
∠3=90°,∠1=∠2=∠3,下列结论:①△ABD为等腰三角形;②AE=AC;③BE=CE=CD;④CB平分∠ACE.其中正确的结论个数有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
可根据证△ABF≌△△ADF推出AB=AD,得出△ABD为等腰三角形;可根据同弦所对的圆周角相等点A、B、C、E共圆,可判出BE=CE=CD,根据三角形内角和等于180°,可判出AE=AC;求出∠7=90°﹣![]() ∠2,根据∠1=∠4=∠2推出∠4≠∠7,即可得出BC不是∠ACE的平分线.
∠2,根据∠1=∠4=∠2推出∠4≠∠7,即可得出BC不是∠ACE的平分线.
解:作AF平分∠BAD,

∵∠BAD=∠3,∠ABD+![]() ∠3=90°,
∠3=90°,
∴∠BAF=![]() ∠3=∠DAF,
∠3=∠DAF,
∴∠ABF+∠BAF=90°
∴∠AFB=∠AFD=90°,
在△BAF和△DAF中

∴△ABF≌△ADF(ASA),
∴AB=AD,∴①正确;
∵∠BAD=∠2=∠3,
∴点A、B、E、C在同一个圆上,
∴∠BAE=∠4=∠3,∠ABC=∠6,
∴BE=CE,
∵∠5=∠ADB=∠ABD,∠BAE=∠4,
∴∠5=∠6,
∴CE=CD,
即CD=CE=BE,∴③正确;
∵∠6+∠2+∠ACE=180°,∠6=∠5=∠ADB=∠ABD=90°﹣![]() ∠2.
∠2.
∴∠ACE=180°﹣∠6﹣∠2=90°﹣![]() ∠2,
∠2,
∴∠ACE=∠6,
∴AE=CE,∴②正确
∵∠5=∠2+∠7=90°﹣![]() ∠2,
∠2,
∴∠7=90°﹣![]() ∠2,
∠2,
∵∠BAD=∠4=∠2,
∴∠4≠∠7,∴④错误;
故选C.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目