题目内容
如图所示,在平面直角坐标系内点A和点C的坐标分别为(4,8),(0,5),过点A作AB⊥x轴于点B ,过OB上的动点D作直线y=kx+b平行于AC,与AB相交于点E,连接CD,过点E作EF∥CD交AC于点F.
,过OB上的动点D作直线y=kx+b平行于AC,与AB相交于点E,连接CD,过点E作EF∥CD交AC于点F.
(1)求经过A、C两点的直线的解析式;
(2)当点D在OB上移动时,能否使四边形CDEF为矩形?若能,求出此时k,b的值;若不能,请说明理由.
 ,过OB上的动点D作直线y=kx+b平行于AC,与AB相交于点E,连接CD,过点E作EF∥CD交AC于点F.
,过OB上的动点D作直线y=kx+b平行于AC,与AB相交于点E,连接CD,过点E作EF∥CD交AC于点F.(1)求经过A、C两点的直线的解析式;
(2)当点D在OB上移动时,能否使四边形CDEF为矩形?若能,求出此时k,b的值;若不能,请说明理由.
(1)设直线AC的解析式为y=kx+b,
∵A(4,8),C(0,5),
∴
,
解得
,
∴直线AC的解析式为:y=
x+5;
(2)∵DE∥AC,直线AC的解析式为:y=
x+5,
∴可设直线DE的解析式为:y=
x+n.
设直线DE与y轴交于点M,则M(0,n),D(-
n,0).
如果四边形CDEF为矩形,则DE⊥CD,
∴∠OCD=∠ODM=90°-∠ODC,
又∵∠COD=∠DOM,
∴△COD∽△DOM,
∴OC:OD=OD:OM,
∴OD2=OC•OM,
∴(-
n)2=5|n|,
∵n<0,解得n=-
,
即直线DE的解析式为:y=
x-
,
故能使四边形CDEF为矩形,此时k=
,b=-
.

∵A(4,8),C(0,5),
∴
|
解得
|
∴直线AC的解析式为:y=
| 3 |
| 4 |
(2)∵DE∥AC,直线AC的解析式为:y=
| 3 |
| 4 |
∴可设直线DE的解析式为:y=
| 3 |
| 4 |
设直线DE与y轴交于点M,则M(0,n),D(-
| 4 |
| 3 |
如果四边形CDEF为矩形,则DE⊥CD,
∴∠OCD=∠ODM=90°-∠ODC,
又∵∠COD=∠DOM,
∴△COD∽△DOM,
∴OC:OD=OD:OM,
∴OD2=OC•OM,
∴(-
| 4 |
| 3 |
∵n<0,解得n=-
| 45 |
| 16 |
即直线DE的解析式为:y=
| 3 |
| 4 |
| 45 |
| 16 |
故能使四边形CDEF为矩形,此时k=
| 3 |
| 4 |
| 45 |
| 16 |


练习册系列答案
相关题目

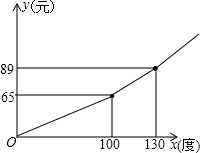


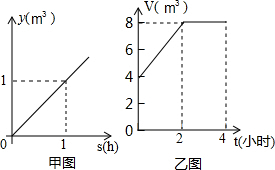
 坐标原点,△PAO的面积为S.
坐标原点,△PAO的面积为S.
