题目内容
【题目】如图,在直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 以
以![]() 的速度运动,同时动点
的速度运动,同时动点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 以
以![]() 的速度向终点
的速度向终点![]() 运动,以
运动,以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() .设平行四边形
.设平行四边形![]() 与直角三角形
与直角三角形![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 运动的时间为
运动的时间为![]() .
.
(1)当点![]() 落在线段
落在线段![]() 上时,求
上时,求![]() 的值;
的值;
(2)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当四边形![]() 为矩形时,直接写出
为矩形时,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;
;![]() ;
;![]() ;(3)
;(3)![]()
【解析】
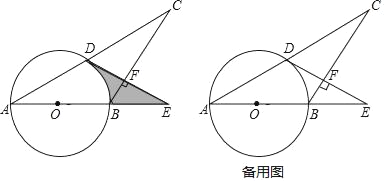
(1)当点E落在线段BC上时,PQ∥BC,得出△APQ∽△ABC,得出
![]() ,由勾股定理得出AC=
,由勾股定理得出AC=![]() =10cm,代入计算得出t=
=10cm,代入计算得出t=![]() ;
;
(2)分情况讨论:①当0<t≤![]() 时,作PG⊥AC于G,证明△APG∽△ACB,得出
时,作PG⊥AC于G,证明△APG∽△ACB,得出![]() ,求出PG=
,求出PG=![]() t,重叠部分图形的面积S=平行四边形PECQ的面积,即可得出结果;
t,重叠部分图形的面积S=平行四边形PECQ的面积,即可得出结果;
②当![]() <t≤5时,作PG⊥AC于G,CF⊥PE于F,则CF=PG,同①得CF=PG=
<t≤5时,作PG⊥AC于G,CF⊥PE于F,则CF=PG,同①得CF=PG=![]() t,PH=10-
t,PH=10-![]() t,得出EH=PE-PH=
t,得出EH=PE-PH=![]() t-10,得出重叠部分图形的面积S=平行四边形PECQ的面积-△CEH的面积,即可得出结果;
t-10,得出重叠部分图形的面积S=平行四边形PECQ的面积-△CEH的面积,即可得出结果;
③当5<t≤6时,Q到达A点停止不动,CE=AP=t,作PG⊥AC于G,同①得:PG=![]() t,BH=
t,BH=![]() t,得出CH=BC-BH=
t,得出CH=BC-BH=![]() t,重叠部分图形的面积为S=平行四边形PECQ的面积-△CEH的面积,即可得出结果;
t,重叠部分图形的面积为S=平行四边形PECQ的面积-△CEH的面积,即可得出结果;
(3)当四边形PECQ为矩形时,∠PQC=90°,证出△APQ∽△ACB,得出![]() ,即可得出结果.
,即可得出结果.
解:(1)当点![]() 落在线段
落在线段![]() 上时,
上时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ;
;
(2)分情况讨论:①当![]() 时,作
时,作![]() 于
于![]() ,如图1所示:
,如图1所示:
图1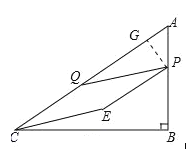
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴重叠部分图形的面积![]() 平行四边形
平行四边形![]() 的面积
的面积![]() ,
,
即![]() ;
;
②当![]() 时,如图2所示:
时,如图2所示:
图2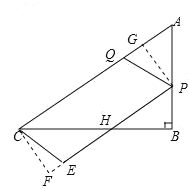
作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
则![]() ,
,
同①得:![]() ,
,![]() ,
,
![]() ,
,
∴重叠部分图形的面积![]() 平行四边形
平行四边形![]() 的面积
的面积![]() 的面积
的面积
![]() ,
,
即![]() ;
;
③当![]() 时,
时,![]() 到达
到达![]() 点停止不动,如图3所示:
点停止不动,如图3所示:
图3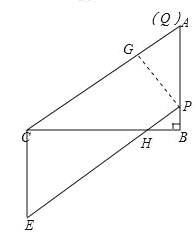
![]() ,作
,作![]() 于
于![]() ,
,
同①得:![]() ,
,![]() ,
,
![]() ,
,
∴重叠部分图形的面积为![]() 平行四边形
平行四边形![]() 的面积
的面积![]() 的面积
的面积
![]() ,
,
即![]() ;
;
(3)当四边形![]() 为矩形时,
为矩形时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
解得:![]() .
.

【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
下面是小东的探究过程,请补充完成:
(1)函数![]() 的自变量x的取值范围是 .
的自变量x的取值范围是 .
(2)在平面直角坐标系xOy中描出了图象上的一些点,请你画出函数的图象;
下表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | 0 | 1 | 1.4 | 2.4 | 2.5 | 3 | 4 | 5 | … |
y | … | ﹣3.25 | ﹣2.33 | ﹣1.50 | ﹣1 | ﹣1.27 | 3.9 | 3.5 | 3 | m | 4.33 | … |
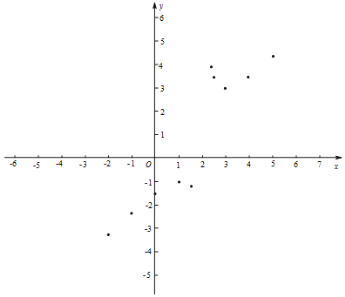
(3)求m的值;
(4)根据图象写出此函数的一条性质.