题目内容
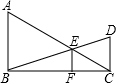
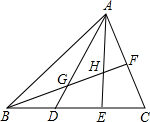
如图,AD是Rt△ABC的斜边BC上的高线,要使△ACD的面积是△ABC和△ABD面积的比例中项,请你添加一个适当的条件:______.


∵AD是Rt△ABC的斜边BC上的高线,
∴S△ABC=
AB•AC=
BC•AD,S△ABD=
AD•BD,S△ACD=
AD•CD,
∵要使△ACD的面积是△ABC和△ABD面积的比例中项,
即S△ACD2=S△ABC•S△ABD,
∴(AD•CD)2=AD•BC•AD•BD,
∴⑥CD2=BC•BD;
∵AB2=BC•BD,
∴①AB=CD;
∵AD2=BD•CD,AC2=BC•CD,
∴③AD2=BD•AB,②AC2=AB•BC;
∵(AD•CD)2=AB•AC•AD•BD,AD2=BD•AB,
∴④CD2=AC•AD;
∴⑤AB2=AD•AC;
有多种答案,如①AB=CD;②AC2=AB•BC;③AD2=BD•AB④CD2=AC•AD;⑤AB2=AD•AC;⑥CD2=BC•BD等等.
故答案为:①AB=CD;②AC2=AB•BC;③AD2=BD.AB④CD2=AC•AD;⑤AB2=AD•AC;⑥CD2=BC•BD.
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵要使△ACD的面积是△ABC和△ABD面积的比例中项,
即S△ACD2=S△ABC•S△ABD,
∴(AD•CD)2=AD•BC•AD•BD,
∴⑥CD2=BC•BD;
∵AB2=BC•BD,
∴①AB=CD;
∵AD2=BD•CD,AC2=BC•CD,
∴③AD2=BD•AB,②AC2=AB•BC;
∵(AD•CD)2=AB•AC•AD•BD,AD2=BD•AB,
∴④CD2=AC•AD;
∴⑤AB2=AD•AC;
有多种答案,如①AB=CD;②AC2=AB•BC;③AD2=BD•AB④CD2=AC•AD;⑤AB2=AD•AC;⑥CD2=BC•BD等等.
故答案为:①AB=CD;②AC2=AB•BC;③AD2=BD.AB④CD2=AC•AD;⑤AB2=AD•AC;⑥CD2=BC•BD.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目