题目内容
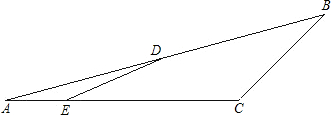
如图所示，在△ABC中，AC=7，BC=4，D为AB的中点，E为AC边上一点，且∠AED=90°+
∠C，求CE的长．
| 1 |
| 2 |
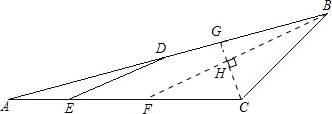
作BF∥DE交AC于F，作∠ACB的平分线交AB于G，交BF于H，
则∠AED=∠AFB=∠CHF+
∠C．
因为∠AED=90°+
∠C，所以∠CHF=90°=∠CHB．
又∠FCH=∠BCH，CH=CH．
∴△FCH≌△BCH．
∴CF=CB=4，
∴AF=AC-CF=7-4=3．
∵AD=DB，BF∥DE，
∴AE=EF=1.5，
∴CE=5.5．
则∠AED=∠AFB=∠CHF+
| 1 |
| 2 |
因为∠AED=90°+
| 1 |
| 2 |
又∠FCH=∠BCH，CH=CH．
∴△FCH≌△BCH．
∴CF=CB=4，
∴AF=AC-CF=7-4=3．
∵AD=DB，BF∥DE，
∴AE=EF=1.5，
∴CE=5.5．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
