题目内容
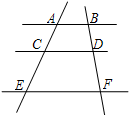
如图,△ABC中,∠B=∠C=30°,AD⊥BC,点O是AD的中点,过O点的直线MN分别交线段AB和AC于点M,N,若AM:MB=3:5,则AN:NC的值是______.
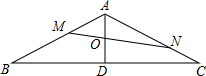

如图,∵∠B=∠C=30°,
∴∠BAC=180°-30°×2=120°,
∵AD⊥BC,
∴∠BAD=∠CAD=
∠BAC=
×120°=60°(等腰三角形三线合一),
过点O作OE∥AC交AB于E,作OF∥AB交AC于F,
则∠AOE=∠CAD=60°,∠AOF=∠BAD=60°,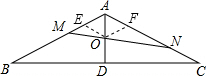
∴△AOE和△AOF都是等边三角形,
∴AE=AE=AO,
∵AM:MB=3:5,
∴AM=3k,MB=5k,
∴AC=AB=3k+5k=8k,
∵∠B=30°,AD⊥BC,
∴AD=
AB=
×8k=4k,
∵点O是AD的中点,
∴AO=
AD=
×4k=2k,
∴ME=AM-AE=3k-2k=k,
∴
=
,
即
=
,
解得AN=6k,
∴NC=AC-AN=8k-6k=2k,
∴AN:NC=6k:2k=3:1.
故答案为:3:1.
∴∠BAC=180°-30°×2=120°,
∵AD⊥BC,
∴∠BAD=∠CAD=
| 1 |
| 2 |
| 1 |
| 2 |
过点O作OE∥AC交AB于E,作OF∥AB交AC于F,
则∠AOE=∠CAD=60°,∠AOF=∠BAD=60°,

∴△AOE和△AOF都是等边三角形,
∴AE=AE=AO,
∵AM:MB=3:5,
∴AM=3k,MB=5k,
∴AC=AB=3k+5k=8k,
∵∠B=30°,AD⊥BC,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
∵点O是AD的中点,
∴AO=
| 1 |
| 2 |
| 1 |
| 2 |
∴ME=AM-AE=3k-2k=k,
∴
| OE |
| AN |
| ME |
| AM |
即
| 2k |
| AN |
| k |
| 3k |
解得AN=6k,
∴NC=AC-AN=8k-6k=2k,
∴AN:NC=6k:2k=3:1.
故答案为:3:1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





 E
E []
[]