��Ŀ����
����Ŀ����֪һ������ֽƬ![]() ������ֽƬ������ƽ��ֱ������ϵ�У���
������ֽƬ������ƽ��ֱ������ϵ�У���![]() ����
����![]() ����PΪ
����PΪ![]() ���ϵĶ���.
���ϵĶ���.
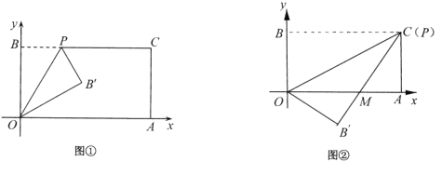
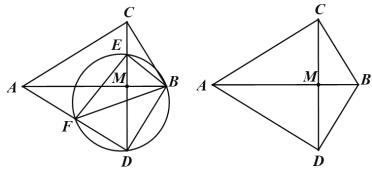
��1����ͼ�٣�������O��P�۵���ֽƬ���õ�![]() ���ۺ�
���ۺ�![]() .����P������Ϊ
.����P������Ϊ![]() ʱ����
ʱ����![]() �Ķ�����
�Ķ�����
��2����ͼ�ڣ�����P���C�غ�ʱ��������O��P�۵�ֽƬ��ʹ��B���ڵ�![]() ��λ�ã�
��λ�ã�![]() ��
��![]() ���ڵ�M�����M�����ꣻ
���ڵ�M�����M�����ꣻ
��3������P��ֱ��![]() ����
����![]() �ڵ�Q����ȡ
�ڵ�Q����ȡ![]() �е�T��
�е�T��![]() �е�N���ֱ���
�е�N���ֱ���![]() ��
��![]() ��
��![]() ��
��![]() Ϊ�ۺۣ������۵���ֽƬ���۵����O�Ķ�Ӧ�����B�Ķ�Ӧ��ǡ���غϣ��������߶�
Ϊ�ۺۣ������۵���ֽƬ���۵����O�Ķ�Ӧ�����B�Ķ�Ӧ��ǡ���غϣ��������߶�![]() �ϣ�A��C�Ķ�Ӧ��Ҳǡ���غϣ�Ҳ�����߶�
�ϣ�A��C�Ķ�Ӧ��Ҳǡ���غϣ�Ҳ�����߶�![]() �ϣ����ʱ��P�����ֱ꣨��д��������ɣ�.
�ϣ����ʱ��P�����ֱ꣨��д��������ɣ�.
���𰸡���1��![]() .��2��
.��2��![]() .��3��
.��3��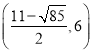 ��
��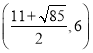 .
.
��������
��1�����������֪��![]() ��
��![]() ��
��![]() ���������к���ֵ��������𰸣�
���������к���ֵ��������𰸣�
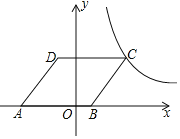
��2��������������֪���Σ���![]() ������
������![]() ����
����![]() �����ù��ɶ������з������㼴�ɣ�
�����ù��ɶ������з������㼴�ɣ�
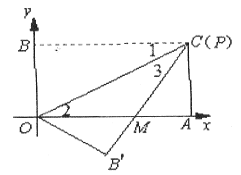
��3�����������P��ֱ��![]() ����
����![]() �ڵ�Q����ȡ
�ڵ�Q����ȡ![]() �е�T��
�е�T��![]() �е�N���ֱ���
�е�N���ֱ���![]() ��
��![]() ��
��![]() ��
��![]() Ϊ�ۺۣ������۵���ֽƬ���з�������.
Ϊ�ۺۣ������۵���ֽƬ���з�������.
�⣺��1�����������֪��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() .
.
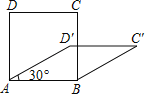
��2������֪���Σ���![]() ��
��
��![]() �������۵�֪
�������۵�֪![]() ��
��
��![]() ��
��
��![]() .
.
��![]() ����
����![]() ����
����![]() ��
�У�
���ݹ��ɶ�����![]() ��
��
��![]() �����
�����![]() .
.
���M������Ϊ![]() .
.
��3��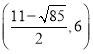 ��
��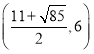 .
.

��ϰ��ϵ�д�
�����Ŀ