题目内容
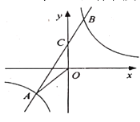
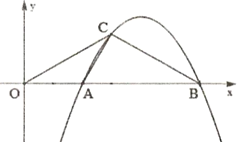
【题目】如图,平面直角坐标系中,点![]() 、点
、点![]() 在
在![]() 轴上(点
轴上(点![]() 在点
在点![]() 的左侧),点
的左侧),点![]() 在第一象限,满足
在第一象限,满足![]() 为直角,且恰使
为直角,且恰使![]() ∽△
∽△![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 、
、![]() 三点.
三点.
(1)求线段![]() 、
、![]() 的长;
的长;
(2)求点![]() 的坐标及该抛物线的函数关系式;
的坐标及该抛物线的函数关系式;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
【答案】(1)OB=6,![]() =
=![]() ;(2)
;(2)![]() 的坐标为
的坐标为![]() ;
;![]() ;(3)存在,
;(3)存在,![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)根据题意先确定OA,OB的长,再根据△OCA∽△OBC,可得出关于OC、OA、OB的比例关系式即可求出线段![]() 、
、![]() 的长;
的长;
(2)由题意利用相似三角形的对应边成比例和勾股定理来求C点的坐标,并将C点坐标代入抛物线中即可求出抛物线的解析式;
(3)根据题意运用等腰三角形的性质,对所有符合条件的![]() 点的坐标进行讨论可知有四个符合条件的点,分别进行分析求解即可.
点的坐标进行讨论可知有四个符合条件的点,分别进行分析求解即可.
解:(1)由![]() (
(![]() )
)
得![]() ,
,![]() ,即:
,即:![]() ,
,![]()
∵![]() ∽
∽![]()
∴![]()
∴![]() (
(![]() 舍去)
舍去)
∴线段![]() 的长为
的长为![]() .
.
(2)∵![]() ∽
∽![]()
∴![]() ,
,![]()
设![]() ,
,
则![]() ,
,
由![]()
得![]() ,
,
解得![]() (-2舍去),
(-2舍去),
∴![]() ,
,![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,
,

由面积得![]() ,∴
,∴![]() 的坐标为
的坐标为![]()
将![]() 点的坐标代入抛物线的解析式得
点的坐标代入抛物线的解析式得![]()
∴![]() .
.
(3)存在![]() ,
,![]() ,
,![]() ,
,![]()
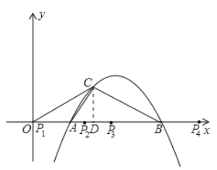
①当P1与O重合时,△BCP1为等腰三角形
∴P1的坐标为(0,0);
②当P2B=BC时(P2在B点的左侧),△BCP2为等腰三角形
∴P2的坐标为(6-2![]() ,0);
,0);
③当P3为AB的中点时,P3B=P3C,△BCP3为等腰三角形
∴P3的坐标为(4,0);
④当BP4=BC时(P4在B点的右侧),△BCP4为等腰三角形
∴P4的坐标为(6+2![]() ,0);
,0);
∴在x轴上存在点P,使△BCP为等腰三角形,符合条件的点P的坐标为:
![]() ,
,![]() ,
,![]() ,
,![]() .
.

【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?