题目内容
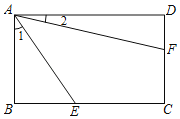
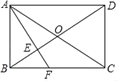
【题目】如图,在矩形ABCD中,对角线AC、BD相交于点O,AF垂直平分OB,交OB于点E,若AB=6,则CF的长为_____.
【答案】4![]()
【解析】
由题意可证△ABO是等边三角形,可得∠BAO=60°,∠BAF=∠CAF=30°,由直角三角形的性质和等腰三角形性质可得BC=![]() AB=6
AB=6![]() ,AF=FC,由勾股定理可求FC的长.
,AF=FC,由勾股定理可求FC的长.
解:∵四边形ABCD是矩形
∴AO=BO=CO=DO,∠ABC=90°
∵AF垂直平分OB,
∴AB=AO,BE=EO,AF⊥BO,
∴AB=AO=BO,
∴△ABO是等边三角形,
∴∠BAO=60°,∠BAF=∠CAF=30°
∴∠ACB=90°﹣∠BAO=30°
∴∠FAC=∠ACF=30°,BC=![]() AB=6
AB=6![]() ,
,
∴AF=FC,
在Rt△ABF中,AF2=BF2+AB2,
∴CF2=(6![]() ﹣CF)2+36
﹣CF)2+36
∴CF=4![]() .
.
故答案是:4![]() .
.

练习册系列答案
相关题目