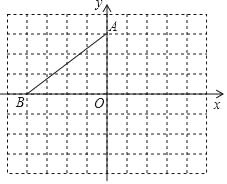
题目内容
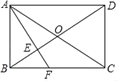
【题目】如图①,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
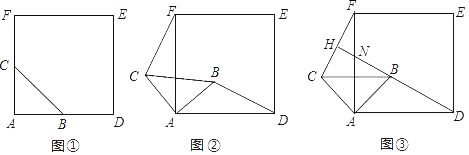
(1)当△ABC绕点A逆时针旋转α(0°<α<90°)时,如图②,BD=CF成立吗?若成立,请证明;若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图③,延长DB交CF于点H;
(ⅰ)求证:BD⊥CF;
(ⅱ)当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
【答案】(1)BD=CF,理由详见解析;(2)(ⅰ)详见解析;(ⅱ)![]() .
.
【解析】
(1)欲证明BD=CF,只要证明△CAF≌△BAD即可;
(2)(ⅰ)由(1)得△CAF≌△BAD,推出∠CFA=∠BDA,由∠FNH=∠DNA,∠DNA+∠NAD=90°,即可推出∠CFA+∠FNH=90°,由此即可解决问题;
(ⅱ)只要证明△DMB∽△DHF,可得![]() ,构建方程即可解决问题;
,构建方程即可解决问题;
(1)BD=CF.
理由如下:由题意得,∠CAF=∠BAD=α,
在△CAF和△BAD中,
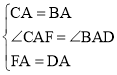 ,
,
∴△CAF≌△BAD,
∴BD=CF.
(2)(ⅰ)由(1)得△CAF≌△BAD,
∴∠CFA=∠BDA,
∵∠FNH=∠DNA,∠DNA+∠NAD=90°,
∴∠CFA+∠FNH=90°,
∴∠FHN=90°,即BD⊥CF.
(ⅱ)连接DF,延长AB交DF于M,

∵四边形ADEF是正方形,AD=3![]() ,AB=2,
,AB=2,
∴AM=DM=3,BM=AM﹣AB=1,
DB=![]()
∵∠MAD=∠MDA=45°,
∴∠AMD=90°,又∠DHF=90°,∠MDB=∠HDF,
∴△DMB∽△DHF,
![]() ,即
,即![]() ,
,
解得,DH=![]() .
.

练习册系列答案
相关题目