��Ŀ����
����Ŀ���Ķ��������ݲ��ش����⣺
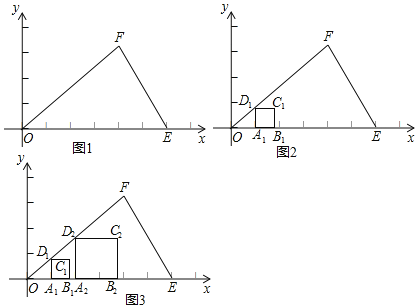
��ͼ1����ƽ��ֱ������ϵxOy�У���һ����OEF��Ҫ���ڡ�OEF����һ���ڽ�������ABCD��ʹ������A��B���������ڡ�OEF��OE���ϣ�����������C��D�ֱ���EF��OF�������ϣ�
С���е�Ҫʹ�ı��ε��ĸ�����ͬʱ��������������Щ���ѣ������������ı��ε��������������������������Ȼ���һ�������������������α��ϵ������Σ���ͼ2�������������ڡ�OEF�ڻ���һ�������������Σ���ͼ3��������������ٶһЩ�����������Σ����ܷ�����Щ��Cλ�õ�����ͼ�Σ��������ͼ�ξ��ܻ��������������������ˣ�
��1������Ҳʵ��һ�£��ٶ���������������Σ�����С��������Щ��C���е�ͼ������ ����
��2������ο�����˼·������������⣺���E��F���������ֱ�ΪE��6��0����F��4��3����
�ٵ�A1�������ǣ�1��0��ʱ����C1���������� ����
�ڵ�A2�������ǣ�2��0��ʱ����C2���������� ����
�۽�ϣ�1���в��룬���������ABCD�Ķ���D�����꣬��ͼ3�л�������������������ABCD��
���𰸡���1��һ���߶Σ���2���٣�![]() ��
��![]() �����ڣ�
�����ڣ�![]() ��
��![]() ����D��������
����D������Ϊ��![]() ��2�����ۼ�����.
��2�����ۼ�����.
��������
��1��ͨ����ͼ����ֱ�ӵó����ۣ�
��2����ȷ����ֱ��OF�Ľ���ʽ��
�ٽ�x��1����ֱ��OF����ʽ���y�����ɵó����ۣ�
�ڽ�x��2����ֱ��OF����ʽ���y�����ɵó����ۣ�
�������ֱ��C1C2�ı���ʽΪy��![]() x��ֱ��EF�ı���ʽΪy����
x��ֱ��EF�ı���ʽΪy����![]() +9���������C������Ϊ��
+9���������C������Ϊ��![]() ��2�������ɵó����ۣ�
��2�������ɵó����ۣ�
�⣺��1��ͨ����ͼ������С��������Щ��C���е�ͼ����һ���߶Σ�
�ʴ�Ϊ��һ���߶Σ�
��2����F��4��3����
��ֱ��OF�ı���ʽ��y��![]() x��
x��
�١��ı���A1B1C1D1�������Σ�
��A1D1��A1B1��
��x��1����ֱ��y��![]() x�У���y��
x����y��![]() ��
��
��OB1��OA1+A1B1��1+![]() ��
��![]() ��
��
��C1�������� ��![]() ��
��![]() ����
����
�ʴ�Ϊ����![]() ��
��![]() ����
����
�ڡ��ı���A2B2C2D2�������Σ�
��A2D2��A2B2��
��x��2����ֱ��y��![]() x�У���y��
x����y��![]() ��
��
��OB2��OA2+A2B2��2+![]() ��
��![]() ��
��
��C2�������� ��![]() ��
��![]() ����
����
�ʴ�Ϊ����![]() ��
��![]() ����
����
�����C1��C2�����һ�κ�������ʽ��y��kx+b��k��0����
����C1��C2�����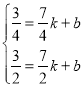 ��
��
���![]() ��
��
��ֱ��C1C2�ı���ʽΪy��![]() x��
x��
���E��6��0����F��4��3�������һ�κ�������ʽ��y��k'x+b'��k'��0����
����E��F�����![]()
��� ��
��
����ֱ��EF�ı���ʽΪy����![]() x+9
x+9
ֱ��EF��y����![]() x+9��ֱ��C1C2��y��
x+9��ֱ��C1C2��y��![]() x�Ľ�������ΪC��
x�Ľ�������ΪC��
����ֱ��EF��ֱ��C1C2����ʽ�ɷ����鲢���ã�x��![]() ��y��2��
��y��2��
��C��������![]() ��2����
��2����
��y��2����y��![]() x�����x��
x�����x��![]() ��
��
��D��������![]() ��2��
��2��
�����ı���ABCD��ͼ3��ʾ��


����Ŀ��ij��˾��![]() ���طֱ������ھ��16̨��12̨�����������ס�������֧Ԯ���裬���м���Ҫ15̨���ҵ���Ҫ13̨.��
���طֱ������ھ��16̨��12̨�����������ס�������֧Ԯ���裬���м���Ҫ15̨���ҵ���Ҫ13̨.��![]() ����һ̨���ס������صķ��÷ֱ���500Ԫ��400Ԫ����
����һ̨���ס������صķ��÷ֱ���500Ԫ��400Ԫ����![]() ����һ̨���ס������ط��÷ֱ���300Ԫ��600Ԫ�����
����һ̨���ס������ط��÷ֱ���300Ԫ��600Ԫ�����![]() ��������
��������![]() ̨�ھ����
̨�ھ����
��1���벹ȫ�±���������������ھ�����ܷ����Ƕ��٣�
�� | �� | �ܼ� | |
|
| ____________̨ | 16̨ |
| _______________̨ | ____________̨ | 12̨ |
�ܼ� | 15̨ | 13̨ | 28̨ |
��2������![]() ��������5̨�ھ��ʱ���������ھ�����ܷ����Ƕ��٣�
��������5̨�ھ��ʱ���������ھ�����ܷ����Ƕ��٣�
��3�������������䷽������ʹ�������ھ�����ܷ������٣����ٷ����Ƕ��٣�