Question

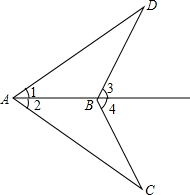如图，∠1=∠2，∠3=∠4，求证：AC=AD  
证明：∵∠

ABD

=180°-∠3
∠

ABC

=180°-∠4
而∠3=∠4（已知）
∴∠ABC=∠ABD
在△ABC和△ABD中
∠1=∠2  （

已知

）
∠ABC=∠ABD （

已证

）

AB=AB

  （

公共边

）
∴△ABC≌△ABD（

ASA

）
∴AC=BD  （

全等三角形对应边相等

）

Answer 1

分析：根据题目推理过程，利用邻补角的定义和全等三角形的判定方法和性质写出理论依据即可．

解答：证明：∵∠ABD=180°-∠3，
∠ABC=180°-∠4，
而∠3=∠4（已知），
∴∠ABC=∠ABD，
在△ABC和△ABD中
∠1=∠2（已知），
AB=AB（公共边），
∠ABC=∠ABD （已证），
∴△ABC≌△ABD（ASA），
∴AC=BD（全等三角形对应边相等）．
故答案为：ABD；ABC；已知；已证；AB=AB；公共边；ASA；全等三角形对应边相等．

点评：本题考查了全等三角形的判定与性质，等角的补角相等的性质，熟练掌握三角形全等的证明是解题的关键．