Question

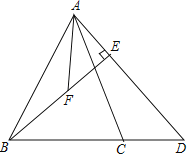
【题目】已知：如图，AB平分∠CBD，∠DBC=60°，∠C＝∠D．

（1）若AC⊥BC，求∠BAE的度数；

（2）请探究∠DAE与∠C的数量关系，写出你的探究结论，并加以证明；

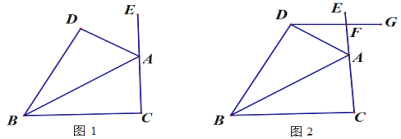
（3）如图，过点D作DG∥BC交CE于点F，当∠EFG＝2∠DAE时，求∠BAD的度数．

Answer 1

【答案】（1）∠BAE＝=120°;（2）结论：∠DAE＝2∠C—120°.证明见解析；（3）∠BAD＝66°.

【解析】

（1）根据角平分线的性质得到∠CBD＝60°，由于∠BAE是△ABC的外角，则可以得到答案.

（2）根据三角形内角和性质和四边形内角和，进行计算即可得到答案.

（3）根据对顶角的性质可得∠EFG＝∠DFA，根据平行线的性质得2∠DAE +∠C=180°，

再根据角平分线的性质即可得到答案.

解：∵AC⊥BC

∴∠BCA＝90°,

∵AB平分∠CBD，

∴∠ABC＝∠CBD, ∠CBD＝60°，

∴∠ABC＝30°，

∵∠BAE是△ABC的外角，

∴∠BAE＝∠BCA+∠ABC=120°.

结论：∠DAE＝2∠C—120°.

证明：∵∠DAE+∠DAC=180°,

∴∠DAC =180°—∠DAE，

∵∠DAC+∠DBC+∠C +∠D =360°,

∴180—∠DAE+∠DBC+∠C +∠D =360°,

∵∠DBC=60°，∠C＝∠D,

∴2∠C—∠DAE=120°,

∴∠DAE＝2∠C—120°.

解：∵∠EFG和∠DFA是对顶角，

∴∠EFG＝∠DFA，

∵∠EFG＝2∠DAE，

∴∠DFA＝2∠DAE，

∵DG∥BC，

∴∠DFA+∠C=180°，

∴2∠DAE +∠C=180°，

∵∠DAE＝2∠C—120°，

∴∠DAE＝48°，

∴∠DAC =132°，

∵AB平分∠CBD，

∴∠DBA＝∠CBA，

∵∠C＝∠D，

∴∠BAD＝∠BAC，

∴∠BAD＝∠DAC=66°